
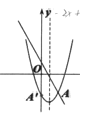
【题目】如图,已知直线y=-2x+1与抛物线y=x2-2x+c的一个交点为点A,作点A关于抛物线对称轴的对称点A,当A刚好落在y轴上时,c的值为____________.
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,⊙O的半径为1,P是坐标系内任意一点,点P到⊙O的距离SP的定义如下:若点P与圆心O重合,则SP为⊙O的半径长;若点P与圆心O不重合,作射线OP交⊙O于点A,则SP为线段AP的长度.
图1为点P在⊙O外的情形示意图.
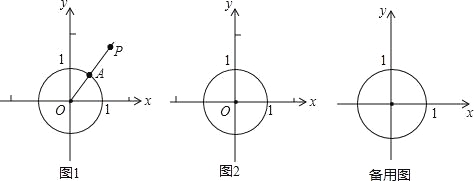
(1)若点B(1,0),C(1,1),D(0,![]() ),则SB= ;SC= ;SD= ;
),则SB= ;SC= ;SD= ;
(2)若直线y=x+b上存在点M,使得SM=2,求b的取值范围;
(3)已知点P,Q在x轴上,R为线段PQ上任意一点.若线段PQ上存在一点T,满足T在⊙O内且ST≥SR,直接写出满足条件的线段PQ长度的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
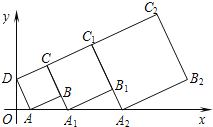
【题目】在平面坐标系中,第1个正方形ABCD的位置如图所示,点A的坐标为(3,0),点D的坐标为(0,4),延长CB交x轴于点A1,作第2个正方形A1B1C1C,延长C1B1交x轴于点A2;作第3个正方形A2B2C2C1,…按这样的规律进行下去,第5个正方形的边长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
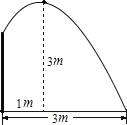
【题目】要修一个圆形喷水池,在池中心竖直安装一根水管,水管的顶端安一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高,高度为3m,水柱落地处离池中心3m,水管应多长?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果批发商销售每箱进价为40元的苹果,物价部门规定每箱售价不得高于55元,市场调查发现,若每箱以50元的价格销售,平均每天销售90箱,价格每提高1元,平均每天少销售3箱.
(1)求平均每天销售量![]() 箱与销售价
箱与销售价![]() 元/箱之间的函数关系式.
元/箱之间的函数关系式.
(2)求该批发商平均每天的销售利润w(元)与销售价![]() (元/箱)之间的函数关系式.
(元/箱)之间的函数关系式.
(3)当每箱苹果的销售价为多少元时,可以获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=-2x+3与抛物线y=x2相交于A,B两点,O为坐标原点.
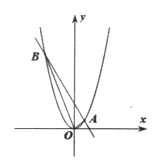
(1)求点A和B的坐标;
(2)连结OA,OB,求△OAB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△BAD是由△BEC在平面内绕点B旋转60°而得,且AB⊥BC,BE=CE,连接DE.
(1)求证:△BDE≌△BCE;
(2)试判断四边形ABED的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店销售一种成本为![]() 元
元![]() 的水产品,若按
的水产品,若按![]() 元
元![]() 销售,一个月可售出
销售,一个月可售出![]() ,售价毎涨
,售价毎涨![]() 元,月销售量就减少
元,月销售量就减少![]() .
.
![]() 写出月销售利润
写出月销售利润![]() (元)与售价
(元)与售价![]() (元
(元![]() )之间的函数表达式;
)之间的函数表达式;
![]() 当售价定为多少元时,该商店月销售利润为
当售价定为多少元时,该商店月销售利润为![]() 元?
元?
![]() 当售价定为多少元时会获得最大利润?求出最大利润.
当售价定为多少元时会获得最大利润?求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面有4个命题:①过任意三点可以画一个圆;②同圆的内接正方形和内接正三角形的边长比是![]() :
:![]() ;③三角形的内心到三角形的三边距离相等;④长度相等的弧是等弧.其中正确的有_____(填序号).
;③三角形的内心到三角形的三边距离相等;④长度相等的弧是等弧.其中正确的有_____(填序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com