
ЁОЬтФПЁПФГЫЎЙћХњЗЂЩЬЯњЪлУПЯфНјМлЮЊ40дЊЕФЦЛЙћЃЌЮяМлВПУХЙцЖЈУПЯфЪлМлВЛЕУИпгк55дЊЃЌЪаГЁЕїВщЗЂЯжЃЌШєУПЯфвд50дЊЕФМлИёЯњЪлЃЌЦНОљУПЬьЯњЪл90ЯфЃЌМлИёУПЬсИп1дЊЃЌЦНОљУПЬьЩйЯњЪл3ЯфЃЎ
ЃЈ1ЃЉЧѓЦНОљУПЬьЯњЪлСП![]() ЯфгыЯњЪлМл
ЯфгыЯњЪлМл![]() дЊ/ЯфжЎМфЕФКЏЪ§ЙиЯЕЪНЃЎ
дЊ/ЯфжЎМфЕФКЏЪ§ЙиЯЕЪНЃЎ
ЃЈ2ЃЉЧѓИУХњЗЂЩЬЦНОљУПЬьЕФЯњЪлРћШѓwЃЈдЊЃЉгыЯњЪлМл![]() ЃЈдЊ/ЯфЃЉжЎМфЕФКЏЪ§ЙиЯЕЪНЃЎ
ЃЈдЊ/ЯфЃЉжЎМфЕФКЏЪ§ЙиЯЕЪНЃЎ
ЃЈ3ЃЉЕБУПЯфЦЛЙћЕФЯњЪлМлЮЊЖрЩйдЊЪБЃЌПЩвдЛёЕУзюДѓРћШѓЃПзюДѓРћШѓЪЧЖрЩйЃП
ЁОД№АИЁПЃЈ1ЃЉгЩЬтвтЕУЃК
y=90-3ЃЈx-50ЃЉ
ЛЏМђЕУЃКy=-3x+240ЃЛ
ЃЈ2ЃЉгЩЬтвтЕУЃК
w=ЃЈx-40ЃЉЃЈ-3x+240ЃЉ
=-3x2+360x-9600ЃЛ
ЃЈ3ЃЉw=-3x2+360x-9600
Ёпa=-3ЃМ0ЃЌ
ЁрХзЮяЯпПЊПкЯђЯТЃЎ
ЕБ![]() ЪБЃЌwгазюДѓжЕЃЎ
ЪБЃЌwгазюДѓжЕЃЎ
гжxЃМ60ЃЌwЫцxЕФдіДѓЖјдіДѓЃЎ
ЁрЕБx=55дЊЪБЃЌwЕФзюДѓжЕЮЊ1125дЊЃЎ
ЁрЕБУПЯфЦЛЙћЕФЯњЪлМлЮЊ55дЊЪБЃЌПЩвдЛёЕУ1125дЊЕФзюДѓРћШѓЃЎ
ЁОНтЮіЁП
ЪдЬтБОЬтЪЧЭЈЙ§ЙЙНЈКЏЪ§ФЃаЭНтД№ЯњЪлРћШѓЕФЮЪЬтЃЎвРОнЬтвтвзЕУГіЦНОљУПЬьЯњЪлСПЃЈyЃЉгыЯњЪлМлxЃЈдЊ/ЯфЃЉжЎМфЕФКЏЪ§ЙиЯЕЪНЮЊy=90Љ3ЃЈxЉ50ЃЉЃЌШЛКѓИљОнЯњЪлРћШѓ=ЯњЪлСПЁСЃЈЪлМлЉНјМлЃЉЃЌСаГіЦНОљУПЬьЕФЯњЪлРћШѓwЃЈдЊЃЉгыЯњЪлМлxЃЈдЊ/ЯфЃЉжЎМфЕФКЏЪ§ЙиЯЕЪНЃЌдйвРОнКЏЪ§ЕФдіМѕадЧѓЕУзюДѓРћШѓЃЎ
НтЃКЃЈ1ЃЉгЩЬтвтЕУЃК
y=90Љ3ЃЈxЉ50ЃЉ
ЛЏМђЕУЃКy=Љ3x+240ЃЛЃЈ3ЗжЃЉ
ЃЈ2ЃЉгЩЬтвтЕУЃК
w=ЃЈxЉ40ЃЉy
ЃЈxЉ40ЃЉЃЈЉ3x+240ЃЉ
=Љ3x2+360xЉ9600ЃЛЃЈ3ЗжЃЉ
ЃЈ3ЃЉw=Љ3x2+360xЉ9600
Ёпa=Љ3ЃМ0ЃЌ
ЁрХзЮяЯпПЊПкЯђЯТЃЎ
ЕБ![]() ЪБЃЌwгазюДѓжЕЃЎ
ЪБЃЌwгазюДѓжЕЃЎ
гжxЃМ60ЃЌwЫцxЕФдіДѓЖјдіДѓЃЎ
ЁрЕБx=55дЊЪБЃЌwЕФзюДѓжЕЮЊ1125дЊЃЎ
ЁрЕБУПЯфЦЛЙћЕФЯњЪлМлЮЊ55дЊЪБЃЌПЩвдЛёЕУ1125дЊЕФзюДѓРћШѓЃЎЃЈ4ЗжЃЉ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
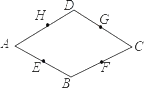
ЁОЬтФПЁПвбжЊЫФБпаЮABCDЮЊСтаЮЃЌЕуEЁЂFЁЂGЁЂHЗжБ№ЮЊИїБпжаЕуЃЌХаЖЯEЁЂFЁЂGЁЂHЫФЕуЪЧЗёдкЭЌвЛИідВЩЯЃЌШчЙћдкЭЌвЛдВЩЯЃЌевЕНдВаФЃЌВЂжЄУїЫФЕуЙВдВЃЛШчЙћВЛдкЃЌЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
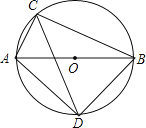
ЁОЬтФПЁПШчЭМЃЌ![]() ЪЧ
ЪЧ![]() ЕФжБОЖЃЌ
ЕФжБОЖЃЌ![]() ЪЧ
ЪЧ![]() ЩЯвЛЕуЃЌ
ЩЯвЛЕуЃЌ![]() дк
дк![]() ЕФбгГЄЯпЩЯЃЌЧв
ЕФбгГЄЯпЩЯЃЌЧв![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓжЄЃК![]() ЪЧ
ЪЧ![]() ЕФЧаЯпЃЛ
ЕФЧаЯпЃЛ
ЃЈ2ЃЉ![]() ЕФАыОЖЮЊ
ЕФАыОЖЮЊ![]() ЃЌ
ЃЌ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФГЄЃЎ
ЕФГЄЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЦћГЕЧхЯДЕъЃЌЧхЯДвЛСОЦћГЕЖЈМл20дЊЪБУПЬьФмЧхЯД45СОЃЌЖЈМл25дЊЪБУПЬьФмЧхЯД30СОЃЌМйЩшЧхЯДЦћГЕСОЪ§![]() ЃЈСОЃЉгыЖЈМл
ЃЈСОЃЉгыЖЈМл![]() ЃЈдЊЃЉЃЈ
ЃЈдЊЃЉЃЈ![]() ШЁећЪ§ЃЉЪЧвЛДЮКЏЪ§ЙиЯЕЃЈЧхЯДУПСОЦћГЕГЩБОКіТдВЛМЦЃЉ.
ШЁећЪ§ЃЉЪЧвЛДЮКЏЪ§ЙиЯЕЃЈЧхЯДУПСОЦћГЕГЩБОКіТдВЛМЦЃЉ.
ЃЈ1ЃЉЧѓ![]() гы
гы![]() жЎМфЕФКЏЪ§БэДяЪНЃЛ
жЎМфЕФКЏЪ§БэДяЪНЃЛ
ЃЈ2ЃЉШєЧхЯДвЛСОЦћГЕЖЈМлВЛЕЭгк15дЊЧвВЛГЌЙ§50дЊЃЌЧвИУЦћГЕЧхЯДЕъУПЬьашжЇИЖЕчЗбЁЂЫЎЗбКЭдБЙЄЙЄзЪЙВМЦ200дЊЃЌЮЪЃКЖЈМлЮЊЖрЩйЪБЃЌИУЦћГЕЧхЯДЕъУПЬьЛёРћзюДѓЃПзюДѓЛёРћЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊжБЯпyЃНЉ2x+6гыХзЮяЯпyЃНax2+bx+cЯрНЛгкAЃЌBСНЕуЃЌЧвЕуAЃЈ1ЃЌ4ЃЉЮЊХзЮяЯпЕФЖЅЕуЃЌЕуBдкxжсЩЯ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉдкЃЈ1ЃЉжаХзЮяЯпЕФЕкШ§ЯѓЯоЭМЯѓЩЯЪЧЗёДцдквЛЕуPЃЌЪЙЁїPOBЁеЁїPOCЃПШєДцдкЃЌЧѓГіЕуPЕФзјБъЃКШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
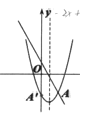
ЁОЬтФПЁПШчЭМ,вбжЊжБЯпy=-2x+1гыХзЮяЯпy=x2-2x+cЕФвЛИіНЛЕуЮЊЕуA,зїЕуAЙигкХзЮяЯпЖдГЦжсЕФЖдГЦЕуA,ЕБAИеКУТфдкyжсЩЯЪБ,cЕФжЕЮЊ____________.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЖўДЮКЏЪ§y=x2+bx+cЕФЭМЯёгыxжсНЛгкAЃЌBСНЕуЃЌBЕузјБъЮЊ(4,0)ЃЌгыyжсНЛгкЕуC(0,4).ЕуDЮЊХзЮяЯпЩЯвЛЕу
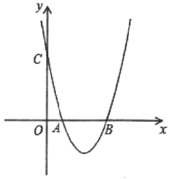
(1)ЧѓХзЮяЯпЕФНтЮіЪНМАAЕузјБъЃЛ
(2)ШєЁїBCDЪЧвдBCЮЊжБНЧБпЕФжБНЧШ§НЧаЮЪБЃЌЧѓЕуDЕФзјБъЃЛ
(3)ШєЁїBCDЪЧШёНЧШ§НЧаЮ,ЧыжБНгаДГіЕуDЕФКсзјБъmЕФШЁжЕЗЖЮЇ .
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПаЁУїДгЖўДЮКЏЪ§y=ax2+bx+cЕФЭМЯѓЃЈШчЭМЃЉжаЙлВьЕУЕНСЫЯТУцЮхЬѕаХЯЂЃКЂйabcЃО0 ЃЛ Ђк2aЉ3b=0 ЃЛ Ђлb2Љ4acЃО0ЃЛЂмa+b+cЃО0ЃЛ Ђн4bЃМc.дђЦфжаНсТле§ШЗЕФИіЪ§ЪЧЃЈЁЁЁЁЃЉ
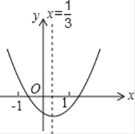
A.2ИіB.3ИіC.4ИіD.5Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌ![]() ЕФжБОЖ
ЕФжБОЖ![]() ЮЊ
ЮЊ![]() ЃЌЯв
ЃЌЯв![]() ЮЊ
ЮЊ![]() ЃЌ
ЃЌ![]() ЕФЦНЗжЯпНЛ
ЕФЦНЗжЯпНЛ![]() гкE,Чв
гкE,Чв![]() .
.
ЃЈ1ЃЉЧѓ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЕФГЄ
ЕФГЄ
ЃЈ2ЃЉЭМжаЛЙгавЛЬѕЯпЖЮ![]() ЕФГЄЪЧЗёФмШЗЖЈЃЌШєФмЧѓГі
ЕФГЄЪЧЗёФмШЗЖЈЃЌШєФмЧѓГі![]() ЕФГЄЁЃ
ЕФГЄЁЃ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com