
【题目】如图,![]() 是
是![]() 的直径,
的直径,![]() 是
是![]() 上一点,
上一点,![]() 在
在![]() 的延长线上,且
的延长线上,且![]() .
.
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)![]() 的半径为
的半径为![]() ,
,![]() ,求
,求![]() 的长.
的长.

【答案】(1)答案见解析;(2)2.
【解析】
(1)连接OC,由AB是⊙O的直径可得出∠ACB=90°,即∠ACO+∠OCB=90°,由等腰三角形的性质结合∠BCD=∠A,即可得出∠OCD=90°,即CD是⊙O的切线;
(2)在Rt△OCD中,由勾股定理可求出OD的值,进而可得出BD的长.
(1)连接OC.
∵AB是⊙O的直径,C是⊙O上一点,∴∠ACB=90°,即∠ACO+∠OCB=90°.
∵OA=OC,∠BCD=∠A,∴∠ACO=∠A=∠BCD,∴∠BCD+∠OCB=90°,即∠OCD=90°,∴CD是⊙O的切线.
(2)在Rt△OCD中,∠OCD=90°,OC=3,CD=4,∴OD=![]() =5,∴BD=OD﹣OB=5﹣3=2.
=5,∴BD=OD﹣OB=5﹣3=2.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
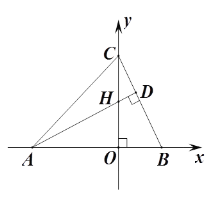
【题目】如图,在平面直角坐标系中AD⊥BC,垂足为D,交y轴于点H,直线BC的解析式为y=-2x+4.点H(0,2),
(1)求证:△AOH≌△COB;
(2)求D点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
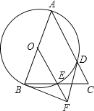
【题目】如图,在等边三角形ABC的外侧作直线AP,点C关于直线AP的对称点为点D,连接AD,BD,其中BD交直线AP于点E.
(1)依题意补全图形;(2)若∠PAC=20°,求∠AEB的度数;
(3)连结CE,写出AE, BE, CE之间的数量关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在![]() 中,
中,![]() ,以
,以![]() 为直径作
为直径作![]() 分别交
分别交![]() ,
,![]() 于
于![]() ,
,![]() 两点,过
两点,过![]() 点的切线交
点的切线交![]() 的延长线于点
的延长线于点![]() .下列结论:
.下列结论:
①![]() ;②两段劣弧
;②两段劣弧![]() =
=![]() ;③
;③![]() 与
与![]() 相切;④
相切;④![]() .
.
其中一定正确的有( )个.
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O是正△ABC内一点,OA=6,OB=8,OC=10,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO',下列结论:①△BO'A可以由△BOC绕点B逆时针旋转60°得到;②点O与O′的距离为6;③∠AOB=150°;④S△BOC=12+6![]() ; ⑤S四边形AOBO′=24+12
; ⑤S四边形AOBO′=24+12![]() .其中正确的结论是_____.(填序号)
.其中正确的结论是_____.(填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
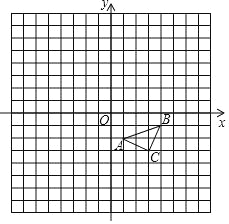
【题目】如图.在平面直角坐标系内,△ABC三个顶点的坐标分别为A(1,﹣2),B(4,﹣1),C(3,﹣3)(正方形网格中,每个小正方形的边长都是1个单位长度).
(1)作出△ABC向左平移5个单位长度,再向下平移3个单位长度得到的△A1B1C1;
(2)以坐标原点O为位似中心,相似比为2,在第二象限内将△ABC放大,放大后得到△A2B2C2作出△A2B2C2;
(3)以坐标原点O为旋转中心,将△ABC逆时针旋转90°,得到△A3B3C3,作出△A3B3C3,并求线段AC扫过的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为落实“美丽抚顺”的工作部署,市政府计划对城区道路进行了改造,现安排甲、乙两个工程队完成.已知甲队的工作效率是乙队工作效率的![]() 倍,甲队改造360米的道路比乙队改造同样长的道路少用3天.
倍,甲队改造360米的道路比乙队改造同样长的道路少用3天.
(1)甲、乙两工程队每天能改造道路的长度分别是多少米?
(2)若甲队工作一天需付费用7万元,乙队工作一天需付费用5万元,如需改造的道路全长1200米,改造总费用不超过145万元,至少安排甲队工作多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,每个小正方形边长都是1.
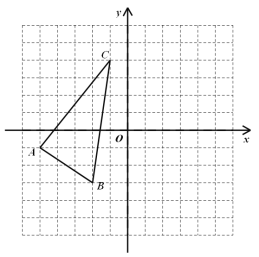
(1)按要求作图: △ABC关于![]() 轴对称的图形△
轴对称的图形△![]() ;
;
(2)将点![]() 先向上平移
先向上平移![]() 个单位,再向右平移
个单位,再向右平移![]() 个单位得到点
个单位得到点![]() 的坐标为 ;
的坐标为 ;
(3)△![]() 的面积为 ;
的面积为 ;
(4)若![]() 为
为![]() 轴上一点,连接
轴上一点,连接![]()
![]() ,则△
,则△![]() 周长的最小值为 .
周长的最小值为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com