
【题目】如图,O是正△ABC内一点,OA=6,OB=8,OC=10,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO',下列结论:①△BO'A可以由△BOC绕点B逆时针旋转60°得到;②点O与O′的距离为6;③∠AOB=150°;④S△BOC=12+6![]() ; ⑤S四边形AOBO′=24+12
; ⑤S四边形AOBO′=24+12![]() .其中正确的结论是_____.(填序号)
.其中正确的结论是_____.(填序号)

【答案】①③
【解析】
证明△BO′A≌△BOC即可说明△BO'A可以由△BOC绕点B逆时针旋转60°得到,①正确;根据旋转的性质可知△BOO′是等边三角形,则点O与O'的距离为8,②错误;根据勾股定理的逆定理得到△AOO′是直角三角形,求得Rt△AOO′面积为![]() ×6×8=24,又等边△BOO′面积为
×6×8=24,又等边△BOO′面积为![]() ×8×4
×8×4![]() =16
=16![]() ,得到四边形AOBO'的面积为24+16
,得到四边形AOBO'的面积为24+16![]() ,⑤错误;求得∠AOB=∠AOO′+∠BOO′=90°+60°=150°,③正确;过B作BE⊥AO交AO的延长线于E,根据三角形的面积公式即可得到S△BOC=S四边形AOBO′﹣S△AOB=24+16
,⑤错误;求得∠AOB=∠AOO′+∠BOO′=90°+60°=150°,③正确;过B作BE⊥AO交AO的延长线于E,根据三角形的面积公式即可得到S△BOC=S四边形AOBO′﹣S△AOB=24+16![]() ﹣12=12+16
﹣12=12+16![]() ,故④错误.
,故④错误.
在△BO′A和△BOC中,
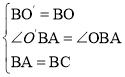 ,
,
∴△BO′A≌△BOC(SAS).
∴O′A=OC,
∴△BO'A可以由△BOC绕点B逆时针旋转60°得到,①正确;
如图1,连接OO′,根据旋转的性质可知△BOO′是等边三角形,
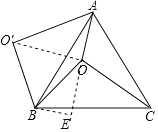
∴点O与O'的距离为8,②错误;
在△AOO′中,AO=6,OO′=8,AO′=10,
∴△AOO′是直角三角形,∠AOO′=90°.
∴Rt△AOO′面积为![]() ×6×8=24,
×6×8=24,
又等边△BOO′面积为![]() ×8×4
×8×4![]() =16
=16![]() ,
,
∴四边形AOBO'的面积为24+16![]() ,⑤错误;
,⑤错误;
∠AOB=∠AOO′+∠BOO′=90°+60°=150°,③正确;
过B作BE⊥AO交AO的延长线于E,
∵∠AOB=150°,
∴∠BOE=30°,
∵OB=8,
∴BE=4,
∴S△AOB=![]() ×4×6=12,
×4×6=12,
∴S△BOC=S四边形AOBO′﹣S△AOB=24+16![]() ﹣12=12+16
﹣12=12+16![]() ,故④错误,
,故④错误,
故答案为:①③.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:
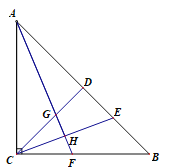
【题目】等腰Rt△ABC,点D为斜边AB上的中点,点E在线段BD上,连结CD,CE,作AH⊥CE,垂足为H,交CD于点G,AH的延长线交BC于点F.
(1)求证:△ADG≌△CDE.
(2)若点H恰好为CE的中点,求证:∠CGF=∠CFG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A、C分别在坐标轴上,点B的坐标为(4,2),直线![]() 交AB,BC分别于点M,N,反比例函数
交AB,BC分别于点M,N,反比例函数![]() 的图象经过点M,N.
的图象经过点M,N.
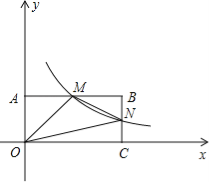
(1)求反比例函数的解析式;
(2)若点P在y轴上,且△OPM的面积与四边形BMON的面积相等,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形DEFG的顶点D、E在△ABC的边BC上,顶点G、F分别在边AB、AC上,如果BC=5,△ABC的面积是10,那么这个正方形的边长是_____.
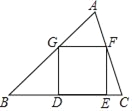
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,点E,F分别在AB,CD上,且![]() ,连接EF交BD于点O连接AO.若
,连接EF交BD于点O连接AO.若![]() ,,则
,,则![]() 的度数为( )
的度数为( )
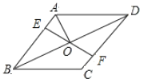
A.50°B.55°C.65°D.75°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ABCD中,∠BAD的平分线交直线BC于点E,交直线DC于点F.
(1)在图1中证明CE=CF;
(2)若∠ABC=90°,G是EF的中点(如图2),直接写出∠BDG的度数;
(3)若∠ABC=120°,FG∥CE,FG=CE,分别连接DB、DG(如图3),求∠BDG的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com