
阅读材料:
已知,如图(1),在面积为S的△ABC中, BC=a,AC=b, AB=c,内切圆O的半径为r.连接OA、OB、OC,△ABC被划分为三个小三角形.
∵  .
.
∴ .
.

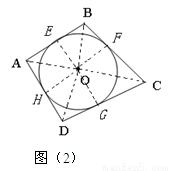
(1)类比推理:若面积为S的四边形ABCD存在内切圆(与各边都相切的圆),如图(2),各边长分别为AB=a,BC=b,CD=c,AD=d,求四边形的内切圆半径r;
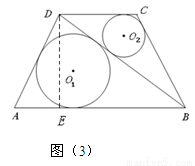
(2)理解应用:如图(3),在等腰梯形ABCD中,AB∥DC,AB=21,CD=11,AD=13,⊙O1与⊙O2分别为△ABD与△BCD的内切圆,设它们的半径分别为r1和r2,求 的值.
的值.
(1)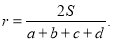 (2)
(2)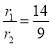 .
.
【解析】
试题分析:(1)如图,连接OA、OB、OC、OD,则△AOB、△BOC、△COD和△DOA都是以点O为顶点、高都是r的三角形,根据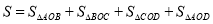 即可求得四边形的内切圆半径r.
即可求得四边形的内切圆半径r.
(2)过点D作DE⊥AB于点E,分别求得AE的长,进而BE 的长,然后利用勾股定理求得BD的长;然后根据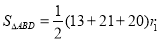 ,
,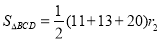 ,两式相除,即可得到
,两式相除,即可得到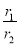 的值.
的值.
试题解析:(1)如图(2),连接OA、OB、OC、OD.···················································1分
∵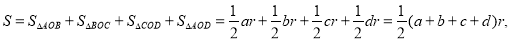 ·3分
·3分
∴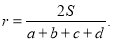 ························································································4分
························································································4分
(2)如图(3),过点D作DE⊥AB于点E,
则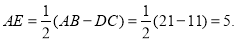
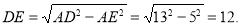
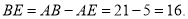
 ·························································6分
·························································6分
∵AB∥DC,∴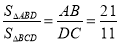 .
.
又∵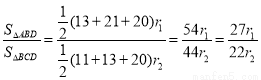 ,
,
∴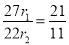 .即
.即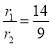 .···········································································9分
.···········································································9分
考点:三角形的内切圆与内心;三角形的面积;勾股定理.


科目:初中数学 来源:2014年初中毕业升学考试(广东汕尾卷)数学(解析版) 题型:解答题
一个口袋中有3个大小相同的小球,球面上分别写有数字1、2、3.从袋中随机地摸出一个小球,记录下数字后放回,再随机地摸出一个小球.
(1)请用树形图或列表法中的一种,列举出两次摸出的球上数字的所有可能结果;
(2)求两次摸出的球上的数字和为偶数的概率.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(山东滨州卷)数学(解析版) 题型:选择题
在△ACB中,∠C=90°,AB=10, ,
, ,
, .则BC的长为( )
.则BC的长为( )
A.6 B.7.5 C.8 D. 12.5
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(山东济宁卷)数学(解析版) 题型:选择题
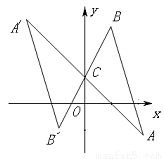
如图,将△ABC绕点C(0,1)旋转180°得到△A'B'C,设点A的坐标为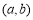 ,则点
,则点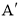 的坐标为( )
的坐标为( )
A. B.
B. C.
C. D.
D.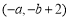
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(四川达州卷)数学(解析版) 题型:解答题
如图,直线L:y=﹣x+3与两坐标轴分别相交于点A、B.
(1)当反比例函数y= (m>0,x>0)的图象在第一象限内与直线L至少有一个交点时,求m的取值范围.
(m>0,x>0)的图象在第一象限内与直线L至少有一个交点时,求m的取值范围.
(2若反比例函数y= (m>0,x>0)在第一象限内与直线L相交于点C、D,当CD=
(m>0,x>0)在第一象限内与直线L相交于点C、D,当CD= 时,求m的值.
时,求m的值.
(3)在(2)的条件下,请你直接写出关于x的不等式﹣x+3< 的解集.
的解集.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com