
°ĺŐ‚ńŅ°Ņő™”≠Ĺ”°įőŚ“Ľ°ĪĻķľ ņÕ∂ĮĹŕ£¨ń≥…Ő≥°ľ∆ĽģĻļĹÝľ◊°Ę““ŃĹ÷÷∆∑Ň∆Ķń![]() –Ű…ņĻ≤100ľĢ£¨“—÷™““∆∑Ň∆√ŅľĢĶńĹÝľŘĪ»ľ◊∆∑Ň∆√ŅľĢĶńĹÝľŘĻů30‘™£¨«“”√120‘™Ļļ¬Úľ◊∆∑Ň∆ĶńľĢ ż«°ļ√ «Ļļ¬Ú““∆∑Ň∆ľĢ żĶń2Ī∂£ģ
–Ű…ņĻ≤100ľĢ£¨“—÷™““∆∑Ň∆√ŅľĢĶńĹÝľŘĪ»ľ◊∆∑Ň∆√ŅľĢĶńĹÝľŘĻů30‘™£¨«“”√120‘™Ļļ¬Úľ◊∆∑Ň∆ĶńľĢ ż«°ļ√ «Ļļ¬Ú““∆∑Ň∆ľĢ żĶń2Ī∂£ģ
£®1£©«ůľ◊°Ę““ŃĹ÷÷∆∑Ň∆√ŅľĢĶńĹÝľŘ∑÷Īū «∂ŗ…Ŕ‘™£Ņ
£®2£©…Ő≥°ĺŲ∂®ľ◊∆∑Ň∆“‘√ŅľĢ50‘™≥Ų Ř£¨““∆∑Ň∆“‘√ŅľĢ100‘™≥Ų Ř£ģő™¬ķ◊„ –≥°–Ť«ů£¨ĻļĹÝľ◊÷÷∆∑Ň∆Ķń żŃŅ≤Ľ…Ŕ”ŕ““÷÷∆∑Ň∆ żŃŅĶń4Ī∂£¨«Žń„»∑∂®ĽŮņŻ◊ÓīůĶńĹÝĽű∑Ĺįł£¨≤Ę«ů≥Ų◊ÓīůņŻ»ů£ģ
°ĺīūįł°Ņ£®1£©ľ◊∆∑Ň∆√ŅľĢĶńĹÝľŘő™30‘™£¨‘Ú““∆∑Ň∆√ŅľĢĶńĹÝľŘő™60‘™£Ľ£®2£©ĻļĹÝľ◊∆∑Ň∆T–Ű…ņ80ľĢ£¨ĻļĹÝ““∆∑Ň∆T–Ű…ņ20ľĢ£¨«“◊ÓīůņŻ»ů «2400‘™
°ĺĹ‚őŲ°Ņ
£®1£©…Ťľ◊∆∑Ň∆√ŅľĢĶńĹÝľŘő™x‘™£¨‘Ú““∆∑Ň∆√ŅľĢĶńĹÝľŘő™£®x+30£©‘™£¨ņŻ”√°į”√120‘™Ļļ¬Úľ◊∆∑Ň∆ĶńľĢ ż«°ļ√ «Ļļ¬Ú““∆∑Ň∆ľĢ żĶń2Ī∂°ĪŃ–∑Ĺ≥Ő«ůĹ‚ľīŅ…£Ľ
£®2£©…Ťł√…Ő≥°ĻļĹÝľ◊∆∑Ň∆T–Ű…ņyľĢ£¨‘ÚĻļĹÝ““∆∑Ň∆T–Ű…ņ£®100-y£©ľĢ£¨ĹŠļŌŐ‚ńŅŐűľĢĶ√ĶĹyĶń∑∂őߣ¨≤ĘŃ–≥ŲņŻ»ů![]() Ļō”ŕyĶń“ĽīőļĮ ż£¨‘ň”√“ĽīőļĮ żĶń–‘÷ ĹŠļŌy∑∂őßľīŅ…«ůĹ‚.
Ļō”ŕyĶń“ĽīőļĮ ż£¨‘ň”√“ĽīőļĮ żĶń–‘÷ ĹŠļŌy∑∂őßľīŅ…«ůĹ‚.
Ĺ‚£ļ£®1£©…Ťľ◊∆∑Ň∆√ŅľĢĶńĹÝľŘő™x‘™£¨‘Ú““∆∑Ň∆√ŅľĢĶńĹÝľŘő™£®x+30£©‘™£¨
”…Ő‚“‚£¨Ķ√![]()
∑Ĺ≥ŐŃĹĪŖ≥ň![]() £¨Ķ√
£¨Ķ√
![]()
Ĺ‚Ķ√![]()
ľž—ť£¨ĶĪ![]() Ī£¨
Ī£¨![]()
ňý“‘£¨‘≠∑÷ Ĺ∑Ĺ≥ŐĶńĹ‚ő™![]()
Ļ ľ◊∆∑Ň∆√ŅľĢĶńĹÝľŘő™30‘™£¨‘Ú““∆∑Ň∆√ŅľĢĶńĹÝľŘő™60‘™.
£®2£©…Ťł√…Ő≥°ĻļĹÝľ◊∆∑Ň∆T–Ű…ņyľĢ£¨‘ÚĻļĹÝ““∆∑Ň∆T–Ű…ņ£®100-y£©ľĢ£¨‘Ú
°ŖĻļĹÝľ◊÷÷∆∑Ň∆Ķń żŃŅ≤Ľ…Ŕ”ŕ““÷÷∆∑Ň∆ żŃŅĶń4Ī∂
°ŗ![]()
°ŗ![]()
”…Ő‚“‚£¨ņŻ»ů![]()
![]()
°Ŗ![]()
°ŗWňśyĶń‘Ųīů∂Ýľű–°
°ŗĶĪ![]() Ī£¨WĶń◊Óīů÷Ķő™
Ī£¨WĶń◊Óīů÷Ķő™![]() ‘™
‘™
°ŗĽŮņŻ◊ÓīůĶńĹÝĽű∑Ĺįł «£ļĻļĹÝľ◊∆∑Ň∆T–Ű…ņ80ľĢ£¨ĻļĹÝ““∆∑Ň∆T–Ű…ņ20ľĢ£¨«“◊ÓīůņŻ»ů «2400‘™.


 ŐžŐžŌÚ…Ō“ĽĪĺļ√ĺŪŌĶŃ–īūįł
ŐžŐžŌÚ…Ō“ĽĪĺļ√ĺŪŌĶŃ–īūįł –°—ß…ķ10∑÷÷””¶”√Ő‚ŌĶŃ–īūįł
–°—ß…ķ10∑÷÷””¶”√Ő‚ŌĶŃ–īūįł
| ńÍľ∂ | łŖ÷–Ņő≥Ő | ńÍľ∂ | ≥ű÷–Ņő≥Ő |
| łŖ“Ľ | łŖ“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű“Ľ | ≥ű“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ∂Ģ | łŖ∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű∂Ģ | ≥ű∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ»ż | łŖ»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű»ż | ≥ű»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° |
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
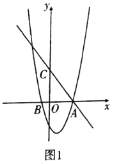
°ĺŐ‚ńŅ°Ņ“—÷™£ļ»ÁÕľ1£¨Ň◊őÔŌŖ![]() «”…Ň◊őÔŌŖ
«”…Ň◊őÔŌŖ![]() ŌÚ”“∆Ĺ“∆1łŲĶ•őĽ£¨‘ŔŌÚŌ¬∆Ĺ“∆4łŲĶ•őĽĶ√ĶĹĶń£¨
ŌÚ”“∆Ĺ“∆1łŲĶ•őĽ£¨‘ŔŌÚŌ¬∆Ĺ“∆4łŲĶ•őĽĶ√ĶĹĶń£¨![]() ”Ž
”Ž![]() ÷ŠĹĽ”ŕ
÷ŠĹĽ”ŕ![]() £¨
£¨![]() ŃĹĶ„£®
ŃĹĶ„£®![]() ‘ŕ
‘ŕ![]() Ķń”“≤ŗ£©£¨÷ĪŌŖ
Ķń”“≤ŗ£©£¨÷ĪŌŖ![]() ĺ≠ĻżĶ„
ĺ≠ĻżĶ„![]() £¨”Ž
£¨”Ž![]() ÷ŠĹĽ”ŕ
÷ŠĹĽ”ŕ![]() Ķ„£ģ
Ķ„£ģ
£®1£©∑÷Īū«ů≥Ų![]() £¨
£¨![]() £¨
£¨![]() Ķń÷Ķ£Ľ
Ķń÷Ķ£Ľ
£®2£©»ÁÕľ2£¨“—÷™![]() Ķ„ «ŌŖ∂ő
Ķ„ «ŌŖ∂ő![]() …Ō»ő“ĽĶ„£®≤Ľ”Ž
…Ō»ő“ĽĶ„£®≤Ľ”Ž![]() £¨
£¨![]() ÷ōļŌ£©£¨Ļż
÷ōļŌ£©£¨Ļż![]() Ķ„◊ų
Ķ„◊ų![]() ÷ŠīĻŌŖ£¨ĹĽŇ◊őÔŌŖ
÷ŠīĻŌŖ£¨ĹĽŇ◊őÔŌŖ![]() ”ŕ
”ŕ![]() Ķ„£ģĶĪ
Ķ„£ģĶĪ![]() ‘ŕļőī¶ Ī£¨ňńĪŖ–ő
‘ŕļőī¶ Ī£¨ňńĪŖ–ő![]() √śĽż◊Óīů£¨«ů≥Ųīň Ī
√śĽż◊Óīů£¨«ů≥Ųīň Ī![]() Ķ„◊ÝĪÍľįňńĪŖ–ő
Ķ„◊ÝĪÍľįňńĪŖ–ő![]() √śĽżĶń◊Óīů÷Ķ£ģ
√śĽżĶń◊Óīů÷Ķ£ģ

≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņňś◊Ň»ň√«Ķń…ķĽÓňģ∆ĹĶńŐŠłŖ£¨ľ“”√Ĺő≥Ķ‘Ĺņī‘Ĺ∂ŗĶōĹÝ»Žľ“Õ•£ģ–°√ųľ“¬ÚŃň“ĽŃĺ–°Ĺő≥Ķ£¨ňŻŃ¨–Ýľ«¬ľŃň7Őž÷–√ŅŐž–– ĽĶń¬∑≥Ő£®»ÁŌ¬ĪŪ£©£¨“‘50kmő™ĪÍ◊ľ£¨∂ŗ”ŕ50kmĶńľ«ő™°į+°Ī£¨≤Ľ◊„50kmĶńľ«ő™°į©Ā°Ī£¨ł’ļ√50kmĶńľ«ő™°į0°Ī£ģ
Ķŕ“ĽŐž | Ķŕ∂ĢŐž | Ķ໿՞ | ĶŕňńŐž | ĶŕőŚŐž | ĶŕŃýŐž | Ķŕ∆ŖŐž | |
¬∑≥Ő£®km£© | ©Ā9 | ©Ā13 | 0 | ©Ā14 | ©Ā16 | +33 | +19 |
£®1£©«ů≥Ų’‚7ŐžĶń–– Ľ¬∑≥Ő÷–◊Ó∂ŗĶń“ĽŐžĪ»◊Ó…ŔĶń“ĽŐž∂ŗ–– Ľ∂ŗ…Ŕ«ß√◊£Ņ
£®2£©»Ű√Ņ–– Ľ100km–Ť”√∆Ż”Õ8…ż£¨√Ņ…ż∆Ż”Õ6.5‘™£¨ľ∆ň„–°√ųľ“’‚7ŐžĶń∆Ż”Õ∑—”√Ļ≤ «∂ŗ…Ŕ‘™£Ņ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ‘ŕ∆Ĺ√ś÷ĪĹ«◊ÝĪÍŌĶńŕ£¨“‘‘≠Ķ„Oő™‘≤–ń£¨1ő™įŽĺ∂◊ų‘≤£¨Ķ„P‘ŕ÷ĪŌŖ![]() …Ō‘ň∂Į£¨ĻżĶ„P◊ųł√‘≤Ķń“ĽŐű«–ŌŖ£¨«–Ķ„ő™A£¨‘ÚPAĶń◊Ó–°÷Ķő™
…Ō‘ň∂Į£¨ĻżĶ„P◊ųł√‘≤Ķń“ĽŐű«–ŌŖ£¨«–Ķ„ő™A£¨‘ÚPAĶń◊Ó–°÷Ķő™![]() °°°°
°°°°![]()
A. 3 B. 2 C. ![]() D.
D. ![]()
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨∂ĢīőļĮ ż![]() ĶńÕľŌů”Žx÷ŠĶń“ĽłŲĹĽĶ„ő™B£®4£¨0£©£¨ŃŪ“ĽłŲĹĽĶ„ő™A£¨«“”Žy÷ŠŌŗĹĽ”ŕCĶ„£ģ
ĶńÕľŌů”Žx÷ŠĶń“ĽłŲĹĽĶ„ő™B£®4£¨0£©£¨ŃŪ“ĽłŲĹĽĶ„ő™A£¨«“”Žy÷ŠŌŗĹĽ”ŕCĶ„£ģ
£®1£©«ůmĶń÷ĶľįCĶ„◊ÝĪÍ£Ľ
£®2£©‘ŕ÷ĪŌŖBC…Ō∑ĹĶńŇ◊őÔŌŖ…Ō «∑Ůīś‘ŕ“ĽĶ„M£¨ ĻĶ√ňŁ”ŽB£¨CŃĹĶ„ĻĻ≥…Ķń»żĹ«–ő√śĽż◊Óīů£¨»Űīś‘ŕ£¨«ů≥Ųīň ĪMĶ„◊ÝĪÍ£Ľ»Ű≤Ľīś‘ŕ£¨«ŽľÚ“™ňĶ√ųņŪ”…£Ľ
£®3£©Pő™Ň◊őÔŌŖ…Ō“ĽĶ„£¨ňŁĻō”ŕ÷ĪŌŖBCĶń∂‘≥∆Ķ„ő™Q£ģ
ĘŔĶĪňńĪŖ–őPBQCő™Ń‚–ő Ī£¨«ůĶ„PĶń◊ÝĪÍ£Ľ
ĘŕĶ„PĶńļŠ◊ÝĪÍő™t£®0£ľt£ľ4£©£¨ĶĪtő™ļő÷Ķ Ī£¨ňńĪŖ–őPBQCĶń√śĽż◊Óīů£¨«ŽňĶ√ųņŪ”…£ģ

≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
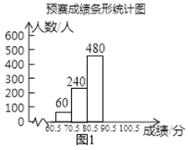
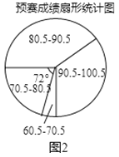
°ĺŐ‚ńŅ°Ņő™ŃňļŽ—Ô÷–Ľ™”Ň–„īęÕ≥őńĽĮ£¨”√ļ√ļļ◊÷£¨ń≥÷–—ßŅ™’ĻŃň“Ľīő°įĻŇ ęī °Ī÷™ ∂ĺļ»Ł£¨»Ł≥ŐĻ≤∑÷°į‘§»Ł°Ęłī»ŁļÕĺŲ»Ł°Ī»żłŲĹ◊∂ő£¨‘§»Ł”…łųįŗĺŔ––£¨»ę‘Ī≤őľ”£¨įīÕ≥“ĽĪÍ◊ľ∆ņ∑÷£¨Õ≥ľ∆≥…ľ®ļůĽś÷∆≥…»ÁÕľ1ļÕÕľ2ňý ĺĶńŃĹ∑ý≤ĽÕÍ’Ż°į‘§»Ł≥…ľ®Őű–őÕ≥ľ∆Õľ°ĪļÕ°į‘§»Ł≥…ľ®…»–őÕ≥ľ∆Õľ°Ī£¨‘§»Ł«į10√Ż—° ÷≤őľ”łī»Ł£¨≥…ľ®ľŻ°į«į10√Ż—° ÷≥…ľ®Õ≥ľ∆ĪŪ°Ī£®≤…”√įŔ∑÷÷∆ľ«∑÷£¨Ķ√∑÷∂ľő™60∑÷“‘…ŌĶń’Ż ż£©.
«į10√Ż—° ÷≥…ľ®Õ≥ľ∆ĪŪ
–ÚļŇ | ĘŔ | Ęŕ | ĘŘ | Ę‹ | Ę› | Ęř | ĘŖ | Ęŗ | ĘŠ | Ę‚ |
‘§»Ł≥…ľ®£®∑÷£© | 100 | 92 | 95 | 98 | 94 | 100 | 93 | 96 | 95 | 96 |
łī»Ł≥…ľ®£®∑÷£© | 90 | 80 | 85 | 90 | 80 | 88 | 85 | 90 | 86 | 89 |
◊‹≥…ľ®£®∑÷£© | 94 | 84.8 | 89 |
| 85.6 | 92.8 | 88.2 |
| 89.6 | 91.8 |
£®1£©«ůł√÷–—ß—ß…ķĶń◊‹»ň ż£¨≤ĘĹęÕľ1≤Ļ≥šÕÍ’Ż£Ľ
£®2£©‘ŕÕľ2÷–£¨«ů°į90.5°ę100.5∑÷ ż∂ő»ň ż°ĪĶń‘≤–ńĹ«∂» ż£Ľ
£®3£©‘§»Ł«į10√Ż—° ÷≤őľ”łī»Ł£¨≥…ľ®ľŻ°į«į10√Ż—° ÷≥…ľ®Õ≥ľ∆ĪŪ°Ī£¨»Űįī‘§»Ł≥…ľ®’ľ40%£¨łī»Ł≥…ľ®’ľ60%ĶńĪ»ņżľ∆ň„◊‹≥…ľ®£¨≤Ęī”÷–—°≥Ų3»ň≤őľ”ĺŲ»Ł£¨ń„»Ōő™—°ńńľłļŇ—° ÷»•≤őľ”ĺŲ»Ł£¨≤ĘňĶ√ųņŪ”….
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņő™Ōž”¶Ķ≥Ķń°įőńĽĮ◊‘–Ň°ĪļŇ’Ŕ£¨ń≥–£Ņ™’ĻŃňĻŇ ęī ň–∂Ńīů»ŁĽÓ∂Į£¨Ō÷ňśĽķ≥ť»°≤Ņ∑÷Õ¨—ßĶń≥…ľ®ĹÝ––Õ≥ľ∆£¨≤ĘĽś÷∆≥…»ÁŌ¬ĶńŃĹłŲ≤ĽÕÍ’ŻĶńÕ≥ľ∆Õľ£¨«ŽĹŠļŌÕľ÷–ŐŠĻ©Ķń–ŇŌĘ£¨Ĺ‚īūŌ¬Ń–łųŐ‚£ļ
£®1£©÷ĪĹ”–ī≥ŲaĶń÷Ķ£¨a=°° °°£¨≤Ęį—∆Ķ ż∑÷≤ľ÷Ī∑ĹÕľ≤Ļ≥šÕÍ’Ż£ģ
£®2£©«ů…»–őBĶń‘≤–ńĹ«∂» ż£ģ
£®3£©»ÁĻŻ»ę–£”–2000√Ż—ß…ķ≤őľ”’‚īőĽÓ∂Į£¨90∑÷“‘…Ō£®ļ¨90∑÷£©ő™”Ň–„£¨ń«√īĻņľ∆ĽŮĶ√”Ň–„ĹĪĶń—ß…ķ”–∂ŗ…Ŕ»ň£Ņ

≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľ1£¨‘ŕ“Ľ’ŇABCDĶń÷Ĺ∆¨÷–£¨ABCDĶń√śĽżő™6£¨DC£Ĺ3£¨°ŌBCD£Ĺ45°„£¨Ķ„P «BD…ŌĶń“Ľ∂ĮĶ„£®Ķ„P”ŽĶ„B£¨D≤Ľ÷ōļŌ£©£ģŌ÷Ĺę’‚’Ň÷Ĺ∆¨∑÷Īū—ōBD£¨APľŰ≥…»żŅť£¨≤ĘįīÕľ2£®◊Ę£ļÕľ2÷–ĶńĘŔ£¨Ęŕ «ĹęÕľ1÷–ĶńĘŔ£¨Ęŕ∑≠◊™Ī≥√ś≥Į…Ō£¨‘Ŕ∆īĹ”∂Ý≥…Ķń£©ňý ĺ∑Ň÷√
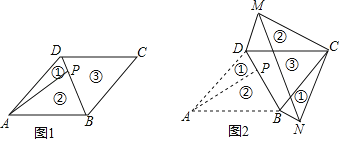
£®1£©ĶĪĶ„P «BDĶń÷–Ķ„ Ī£¨«ůAPĶń≥§£ģ
£®2£© ‘ŐĹĺŅ£ļĶĪĶ„P‘ŕBDĶń ≤√īőĽ÷√…Ō Ī£¨MNĶń≥§◊Ó–°£Ņ«Ž«ů≥Ų’‚łŲ◊Ó–°÷Ķ£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
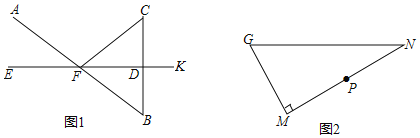
°ĺŐ‚ńŅ°Ņ£®1£©»ÁÕľ1£¨“—÷™EKīĻ÷Ī∆Ĺ∑÷BC£¨īĻ◊„ő™D£¨AB”ŽEKŌŗĹĽ”ŕĶ„F£¨Ń¨Ĺ”CF£ģ«ů÷§£ļ°ŌAFE=°ŌCFD£ģ
£®2£©»ÁÕľ2£¨‘ŕRt°ųGMN÷–£¨°ŌM=90°„£¨Pő™MNĶń÷–Ķ„£ģ
ĘŔ”√÷Ī≥ŖļÕ‘≤Ļś‘ŕGNĪŖ…Ō«ů◊ųĶ„Q£¨ ĻĶ√°ŌGQM=°ŌPQN£®Ī£ŃŰ◊ųÕľļŘľ££¨≤Ľ“™«ů–ī◊ų∑®£©£Ľ
Ęŕ‘ŕĘŔĶńŐűľĢŌ¬£¨»ÁĻŻ°ŌG=60°„£¨ń«√īQ «GNĶń÷–Ķ„¬ū£Ņő™ ≤√ī£Ņ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ļķľ —ß–£”Ň—° - Ń∑Ōį≤ŠŃ–ĪŪ - ‘Ő‚Ń–ĪŪ
ļĢĪĪ °Ľ•Ń™ÕÝő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®∆ĹŐ® | ÕÝ…Ō”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | ĶÁ–Ň’©∆≠ĺŔĪ®◊®«Ý | …śņķ ∑–ťőř÷ų“Ś”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | …ś∆ů«÷»®ĺŔĪ®◊®«Ý
ő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®ĶÁĽį£ļ027-86699610 ĺŔĪ®” Ōš£ļ58377363@163.com