练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如果方程－8=－的解与方程4x－(3a＋1)=6x＋2a－1的解相同，求式子a2＋a＋1的值．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：湖北省宜城市2019届九年级上学期期中考试数学试卷 题型：解答题

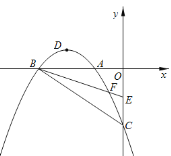
    如图，在平面直角坐标系中，已知抛物线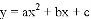（a≠0）与x轴交于A（﹣1，0）、B（﹣3，0）两点，与y轴交于点C（0，﹣3），其顶点为点D，点E的坐标为（0，﹣），该抛物线与BE交于另一点F，连接BC．

    （1）求该抛物线的解析式，并用配方法把解析式化为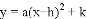的形式；

    （2）动点M从点D出发，沿抛物线对称轴方向向上以每秒1个单位的速度运动，运动时间为t，连接OM，BM，当t为何值时，△OMB为等腰三角形？（3）在x轴上方的抛物线上，是否存在点P，使得∠PBF被BA平分？若存在，请求出点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源：2018-2019学年湖北省人教版八年级（上）第一次月考数学试卷 题型：解答题

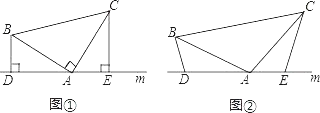
    （1）已知，如图①，在△ABC中，∠BAC＝90°，AB＝AC，直线m经过点A，BD⊥直线m，CE⊥直线m，垂足分别为点D、E，求证：DE＝BD+CE．

    （2）如图②，将（1）中的条件改为：在△ABC中，AB＝AC，D、A、E三点都在直线m上，并且有∠BDA＝∠AEC＝∠BAC＝α，其中α为任意钝角，请问结论DE＝BD+CE是否成立？若成立，请你给出证明：若不成立，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源：2018-2019学年湖北省人教版八年级（上）第一次月考数学试卷 题型：单选题

    已知△ABC的∠A=60°，剪去∠A后得到一个四边形，则∠1+∠2的度数为( )

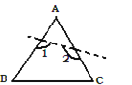
    A. 270° B. 240° C. 200° D. 180°

    查看答案和解析>>

    科目：初中数学 来源：七年级数学阶段检测卷 (第4、5章) 题型：解答题

    用正方形硬纸板做三棱柱盒子，每个盒子由3个矩形侧面和2个正三角形底面组成。硬纸板以如图两种方式裁剪（裁剪后边角料不再利用）

    A方法：剪6个侧面； B方法：剪4个侧面和5个底面。

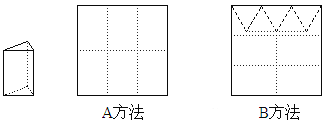
    现有19张硬纸板，裁剪时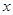张用A方法，其余用B方法。

    （1）用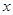的代数式分别表示裁剪出的侧面和底面的个数；

    （2）若裁剪出的侧面和底面恰好全部用完，问能做多少个盒子？

    查看答案和解析>>

    科目：初中数学 来源：七年级数学阶段检测卷 (第4、5章) 题型：填空题

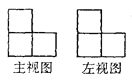
    若由一些完全相同的小正方体搭成的几何体的主视图和左视图如图所示，则组成这个几何体的小正方体的个数最多是_________．

    查看答案和解析>>

    科目：初中数学 来源：七年级数学阶段检测卷 (第4、5章) 题型：填空题

    下列各图中， 不是正方体的展开图（填序号）．

    查看答案和解析>>

    科目：初中数学 来源：广西桂林市灌阳县2018-2019学年八年级上学期期中考试数学试卷 题型：解答题

    计算：（1） （2）

    （3） （4）

    查看答案和解析>>

    科目：初中数学 来源：江苏省江阴市澄西片2018-2019学年八年级上学期期中考试数学试卷 题型：单选题

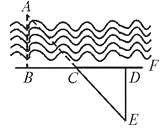
    要测量河两岸相对的两点A、B的距离，先在AB的垂线BF上取两点C、D，使CD=BC，再定出BF的垂线DE，使A、C、E在一条直线上，可以证明△EDC≌△ABC，得到ED=AB，因此测得ED的长就是AB的长（如图）.判定△EDC≌△ABC的理由是

    A. 边角边公理 B. 角边角公理

    C. 边边边公理 D. 斜边直角边公理

    查看答案和解析>>

    同步练习册答案