
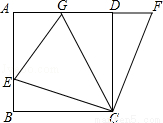
如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.
(1)求证:CE=CF;(2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?
(1)证明见解析;
(2)GE=BE+GD成立.理由见解析.
【解析】
试题分析:(1)由DF=BE,四边形ABCD为正方形可证△CEB≌△CFD,从而CE=CF;
(2)由CE=CF,∠BCE+∠ECD=∠DCF+∠ECD即∠ECF=∠BCD=90°又∠GCE=45°所以可得∠GCE= ∠GCF,故可证得△ECG≌△FCG,即EG=FG=GD+DF.又因为DF=BE,可证出GE=BE+GD成立.
试题解析:(1)在正方形ABCD中,
∵ ,
,
∴△CBE≌△CDF(SAS).
∴CE=CF;
(2)GE=BE+GD成立.理由是:
∵△CBE≌△CDF,
∴∠BCE=∠DCF,
∴∠BCE+∠ECD=∠DCF+∠ECD,即∠ECF=∠BCD=90°,
又∵∠GCE=45°,∴∠GCF=∠GCE=45°.
∵ ,
,
∴△ECG≌△FCG(SAS).
∴GE=GF.
∴GE=DF+GD=BE+GD.
考点:1.正方形的性质2.全等三角形的判定与性质.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:2016届北京市七年级下学期期末数学试卷(解析版) 题型:解答题
列一元一次不等式(组)解决实际问题:
元旦联欢会上,班级为同学们买了一批小礼物,如果每个人分3个,还多5个;如果每个人分4个,就会有一个人能分到但分不到4个,若已知班级学生的人数是奇数,试问这些小礼物共有多少个?
查看答案和解析>>
科目:初中数学 来源:2016届北京市七年级下学期期末数学试卷(解析版) 题型:选择题
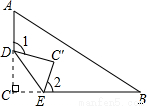
已知Rt△ABC中,∠C=90°,将∠C沿DE向三角形内折叠,使点C落在△ABC的内部,如图,则∠1+∠2=( )
A.90° B.135° C.180° D.270°
查看答案和解析>>
科目:初中数学 来源:2016届北京市七年级下学期期末数学试卷(解析版) 题型:选择题
若点P(1-m,2m-4)在第四象限内,则m的取值范围是( )
A.m<1 B.1<m<2 C.m<2 D.m>2
查看答案和解析>>
科目:初中数学 来源:2015届重庆市合川区第五学区八年级下学期半期考试数学试卷(解析版) 题型:选择题
如图,有两颗树,一颗高10米,另一颗高4米,两树相距8米.一只鸟从一颗树的树梢飞到另一颗树的树梢,问小鸟至少飞行( )

A.8米 B.10米 C.12米 D.14米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com