
分析 首先分别估算出$\sqrt{2}$和3$\sqrt{3}$的大小,然后根据数轴的特征,判断出A,B两点间表示的整数的点共有多少个即可.
解答 解:∵$\sqrt{2}$≈1.414,3$\sqrt{3}$≈3×1.732=5.196,
∴A,B两点间表示的整数的点共有4个:2、3、4、5.
故答案为:4.
点评 (1)此题主要考查了实数与数轴问题,要熟练掌握,解答此题的关键是要明确:实数与数轴上的点是一一对应关系.任意一个实数都可以用数轴上的点表示;反之,数轴上的任意一个点都表示一个实数.数轴上的任一点表示的数,不是有理数,就是无理数.
(2)此题还考查了估算无理数的大小的方法,要熟练掌握.


科目:初中数学 来源: 题型:选择题
| A. | 2≤a<3 | B. | 2<a<3 | C. | -3<a<-2 | D. | -3≤a<2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
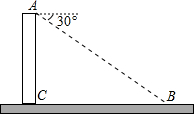 如图,为了测量楼的高度,自楼的顶部A看地面上的一点B,俯角为30°,已知地面上的这点与楼的水平距离BC为30m,那么楼的高度AC为10$\sqrt{3}$m(结果保留根号).
如图,为了测量楼的高度,自楼的顶部A看地面上的一点B,俯角为30°,已知地面上的这点与楼的水平距离BC为30m,那么楼的高度AC为10$\sqrt{3}$m(结果保留根号).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com