练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知三角形的两边长分别为2和4，第三边的长是方程x2﹣4x+3=0的解，则这个三角形的周长为（ ）
    A.3
    B.9
    C.7或9
    D.7

    【答案】B
    【解析】解：x2﹣4x+3=0， （x﹣1）（x﹣3）=0，
    x﹣1=0或x﹣3=0，
    所以x1=1，x2=3，
    因为1+2＜4，
    所以三角形第三边长为3，
    所以三角形的周长为2+3+4=9．
    故选B．
    【考点精析】通过灵活运用三角形三边关系，掌握三角形两边之和大于第三边；三角形两边之差小于第三边；不符合定理的三条线段，不能组成三角形的三边即可以解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】分解因式：xy2﹣x= ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

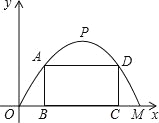
    【题目】施工队要修建一个横断面为抛物线的公路隧道，其高度为6米，宽度OM为12米，现在O点为原点，OM所在直线为x轴建立直角坐标系（如图所示）．

    （1）直接写出点M及抛物线顶点P的坐标；

    （2）求出这条抛物线的函数解析式；

    （3）施工队计划在隧道门口搭建一个矩形“脚手架”ABCD，使A、D点在抛物线上，B、C点在地面OM上．为了筹备材料，需求出“脚手架”三根木杆AB、AD、DC的长度之和的最大值是多少？请你帮施工队计算一下．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列判断正确的是（　　）

    A. 两边和一角对应相等的两个三角形全等 B. 一边及一锐角相等的两个直角三角形全等

    C. 顶角和底边分别相等的两个等腰三角形全等 D. 三个内角对应相等的两个三角形全等

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB和DE是直立在地面上的两根立柱．AB=4m，某一时刻AB在阳光下的投影BC=3m．

    （1）请你在图中画出此时DE在阳光下的投影．

    （2）在测量AB的投影时，同时测量出DE在阳光下的投影长为8m，请你计算DE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在直角坐标系中，将坐标是（3，0），（3，2），（0，3），（3，5），（3，2），（6，3），（6，2），（3，0），（6，0）的点用线段依次连接起来形成一个图案．

    （1）作出原图案关于x轴对称的图案．两图案中的对应点的坐标有怎样的关系？

    （2）作出原图案关于y轴对称的图案．两图案中的对应点的坐标有怎样的关系？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小明、小刚和小红打算各自随机选择本周日的上午或下午去兴化李中水上森林游玩．

    （1）小明和小刚都在本周日上午去游玩的概率为 ；

    （2）求他们三人在同一个半天去游玩的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】计算6a2-5a+3与5a2+2a-1的差，结果正确的是（ ）
    A.a2-3a+4
    B.a2-3a+2
    C.a2-7a+2
    D.a2-7a+4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知在平面直角坐标系xOy中，O为坐标原点，线段AB的两个端点A（0，2），B（1，0）分别在y轴和x轴的正半轴上，点C为线段AB的中点，现将线段BA绕点B按顺时针方向旋转90°得到线段BD，抛物线y=ax2+bx+c（a≠0）经过点D．

    （1）如图1，若该抛物线经过原点O，且a=﹣．

    ①求点D的坐标及该抛物线的解析式；

    ②连结CD，问：在抛物线上是否存在点P，使得∠POB与∠BCD互余？若存在，请求出所有满足条件的点P的坐标，若不存在，请说明理由；

    （2）如图2，若该抛物线y=ax2+bx+c（a≠0）经过点E（1，1），点Q在抛物线上，且满足∠QOB与∠BCD互余．若符合条件的Q点的个数是3个，请直接写出a的值．

    查看答案和解析>>

    同步练习册答案