
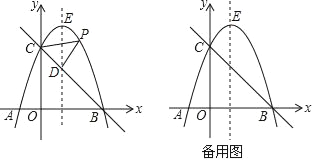
【题目】如图,在平面直角坐标系中,抛物线y=ax2+2x+c与x轴交A(﹣1,0),B两点,与y轴交于点C(0,3),抛物线的顶点为点E.
(1)求抛物线的解析式;
(2)经过B,C两点的直线交抛物线的对称轴于点D,点P为直线BC上方抛物线上的一个动点,当点P运动到点E时,求△PCD的面积;
(3)点N在抛物线对称轴上,点M在x轴上,是否存在这样的点M与点N,使以M,N,C,B为顶点的四边形是平行四边形?若存在,请直接写出点M的坐标(不写求解过程);若不存在,请说明理由.
【答案】(1) y=﹣x+2x+3;(2)1;(3)见解析.
【解析】
(1)由点 A,C 的坐标,利用待定系数法即可求出抛物线的解析式;(2)利用二次函数图象上点的坐标特征可求出点 B 的坐标,利用配方法可求出顶点 E 的坐标,由点 B,C 的坐标,利用待定系数法可求出直线 BC 的解析式, 利用一次函数图象上点的坐标特征可得出点 D 的坐标,再利用三角形的面积公式即可求出当点 P 运动到点 E 时△PCD 的面积;(3)设点 M 的坐标为(m,0),点 N 的坐标为(1,n),分四边形 CBMN 为平行四边形、四边形 CMNB 为平行四边形及四边形 CMBN 为平行四边形三种情况,利用平行四边形的性质找出关于 m 的一元一次方程,解之即可得出结论.
(1)将 A(﹣1,0),C(0,3)代入 y=ax2+2x+c,得:
![]() ,解得:
,解得:![]() ,
,
∴抛物线的解析式为 y=﹣x2+2x+3.
(2)当 y=0 时,有﹣x2+2x+3=0, 解得:x1=﹣1,x2=3,
∴点 B 的坐标为(3,0).
∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴点 E 的坐标为(1,4).
设过 B,C 两点的直线解析式为 y=kx+b(k≠0),将 B(3,0),C(0,3)代入 y=kx+b,得:![]() ,解得:
,解得:![]() ,
,
∴直线 BC 的解析式为 y=﹣x+3.
∵点 D 是直线与抛物线对称轴的交点,
∴点 D 的坐标为(1,2),
∴DE=2,
∴当点 P 运动到点 E 时,△PCD 的面积=![]() ×2×1=1.
×2×1=1.
(3)设点 M 的坐标为(m,0),点 N 的坐标为(1,n).分三种情况考虑:
①当四边形 CBMN 为平行四边形时,有 1﹣0=m﹣3, 解得:m=4,
∴此时点 M 的坐标为(4,0);
②当四边形 CMNB 为平行四边形时,有 m﹣1=0﹣3, 解得:m=﹣2,
∴此时点 M 的坐标为(﹣2,0);
③当四边形 CMBN 为平行四边形时,有 0﹣1=m﹣3, 解得:m=2,
∴此时点 M 的坐标为(2,0).
综上所述:存在这样的点 M 与点 N,使以 M,N,C,B 为顶点的四边形是平行四边形,点 M 的坐标为(4,0)或(﹣2,0)或(2,0).


科目:初中数学 来源: 题型:
【题目】如图,等边三角形的顶点A(1,1)、B(3,1),规定把等边△ABC“先沿y轴翻折,再向下平移1个单位”为一次变换,如果这样连续经过2020次变换后,等边△ABC的顶点C的坐标为____.
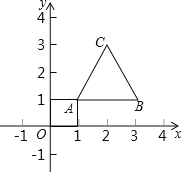
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c与x轴交于点A(-1,0),顶点坐标(1,n)与y轴的交点在(0,2),(0,3)之间(包含端点),则下列结论:①3a+b<0;②-1≤a≤-![]() ;③对于任意实数m,a+b≥am2+bm总成立;④关于x的方程ax2+bx+c=n-1有两个不相等的实数根.其中结论正确的个数为( )
;③对于任意实数m,a+b≥am2+bm总成立;④关于x的方程ax2+bx+c=n-1有两个不相等的实数根.其中结论正确的个数为( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明与小刚玩掷骰子游戏,按所得的数字是几,棋子就向前走几格,每人可连续投掷两次,棋子最终落到哪一格,就可获得相应格子中的奖品.现在轮到小明掷骰子,棋子处于如图所示的地方.
求:(1)小明掷一次骰子能得到奖品吗?
(2)小明下一次投掷有没有可能获得奖品?若能获奖,概率是多少?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
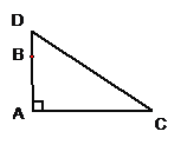
【题目】如图:在一棵树的10m高的B处有两只猴子,其中一只爬下树走向离树20m的池塘C.而另一只猴子爬到树顶D沿直线DC进入池塘,结果两只猴子经过的路程相等,则树有多高?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一张月历表,在此月历表上用一个正方形任意圈出 2×2个数(如 1,2,8,9), 如果圈出的四个数中的最小数与最大数的积为 308,那么这四个数的和为( )
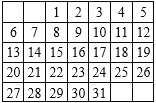
A.68B.72C.74D.76
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,丁轩同学在晚上由路灯AC走向路灯BD,当他走到点P时,发现身后他影子的顶部刚好接触到路灯AC的底部,当他向前再步行20m到达Q点时,发现身前他影子的顶部刚好接触到路灯BD的底部,已知丁轩同学的身高是1.5m,两个路灯的高度都是9m,则两路灯之间的距离是( )

A. 24m B. 25m C. 28m D. 30m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进一批L型服装(数量足够多),进价为40元/件,以60元/件销售,每天销售20件。根据市场调研,若每件每降1元,则每天销售数量比原来多3件。现商场决定对L型服装开展降价促销活动,每件降价x元(x为正整数)。在促销期间,商场要想每天获得最大销售利润,每件降价多少元?每天最大销售毛利润为多少?(注:每件服装销售毛利润指每件服装的销售价与进货价的差)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com