
【题目】在ABCD中,对角线AC,BD相交于点O,点E,F在AC上且AE=CF,
证明:DE=BF.
【答案】证明:∵连接BE,DF,
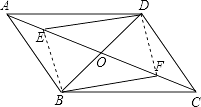
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵AE=CF,
∴OA﹣AE=OC﹣CF,
∴OE=OF,
∴四边形BEDF是平行四边形,
∴DE=BF.
【解析】方法一、连接BE,DF,利用平行四边形的性质及判定去证明四边形BEDF是平行四边形,就可以得出结论。
方法二、根据平行四边形的性质及已知条件,先证明OB=OD、OF=OE,再证明△ODE≌△OBF,即可求证结论。
【考点精析】根据题目的已知条件,利用平行四边形的判定与性质的相关知识可以得到问题的答案,需要掌握若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:初中数学 来源: 题型:
【题目】如图,在边长为 2 的正方形 ABCD 中剪去一个边长为 1 的小正方形 EFGD ,动点 P 从点 A 出发,沿A E F G C B 的路线,绕多边形的边匀速运动到点 B 时停止,则 ABP 的面积 S 随着时间t 变化的函数图象大致是( )

A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系xOy中,直线AB与x轴交于点A(﹣2,0),与反比例函数在第一象限内的图象的交于点B(2,n),连接BO,若S△AOB=4.
(1)求该反比例函数的解析式和直线AB的解析式;
(2)若直线AB与双曲线的另一交点为D点,求△ODB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
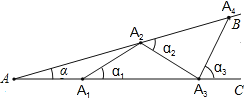
【题目】如图所示,设∠BAC=α(0°![]() α
α![]() 90°),现把等长的小棒依次向右摆放在两射线之间,并使小棒两端分别落在射线AB,AC上,从点A1开始,其中A1A2为第一根小棒,且A1A2=AA1.
90°),现把等长的小棒依次向右摆放在两射线之间,并使小棒两端分别落在射线AB,AC上,从点A1开始,其中A1A2为第一根小棒,且A1A2=AA1.
(1)若已经摆放了3根小棒,则∠α1= ;∠α2= ;(用含α的式子表示),若A4A3C=92°,求∠BAC的度数.
(2)若只能摆放6根小棒,求α的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D是给定△ABC边BC所在直线上一动点,E是线段AD上一点,DE=2AE,连接BE,CE,点D从B的左边开始沿着BC方向运动,则△BCE的面积变换情况是( )
A.逐渐变大
B.逐渐变小
C.先变小后变大
D.始终不变
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为给人们的生活带来方便,2017年兴化市准备在部分城区实施公共自行车免费服务.图1是公共自行车的实物图,图2是公共自行车的车架示意图,点A,D,C,E在同一条直线上,CD=35cm,DF=24cm,AF=30cm,FD⊥AE于点D,座杆CE=15cm,且∠EAB=75°.
(1)求AD的长;
(2)求点E到AB的距离(结果保留整数).
(参考数据:sin75°≈0.97,cos75°≈0.26,tan75°≈3.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂设门市部专卖某产品,该每件成本每件成本30元,从开业一段时间的每天销售统计中,随机抽取一部分情况如下表所示:
销售单位(元) | 50 | 60 | 70 | 75 | 80 | 85 | … |
日销售量 | 300 | 240 | 180 | 150 | 120 | 90 | … |
假设每天定的销价是不变的,且每天销售情况均服从这种规律.
(1)秋日销售量与销售价格之间满足的函数关系式;
(2)门市部原设定两名销售员,担当销售量较大时,在每天售出量超过198件时,则必须增派一名营业员才能保证营业有序进行.设营业员每人每天工资为40元,求每件产品应定价多少元,才能使每天门市部纯利润最大?(纯利润=总销售﹣成本﹣营业员工资)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,![]() 的顶点都在格点上,建立平面直角坐标系,
的顶点都在格点上,建立平面直角坐标系,
(1)点A的坐标为______,点C的坐标为______;
(2)将![]() 先向右平移2个单位长度,再向下平移3个单位长度,请画出平移后的
先向右平移2个单位长度,再向下平移3个单位长度,请画出平移后的![]() ,并分别写出点A1、B1、C1的坐标;
,并分别写出点A1、B1、C1的坐标;
(3)求![]() 的面积.
的面积.
 0
0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com