
【题目】如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,![]() 的顶点都在格点上,建立平面直角坐标系,
的顶点都在格点上,建立平面直角坐标系,
(1)点A的坐标为______,点C的坐标为______;
(2)将![]() 先向右平移2个单位长度,再向下平移3个单位长度,请画出平移后的
先向右平移2个单位长度,再向下平移3个单位长度,请画出平移后的![]() ,并分别写出点A1、B1、C1的坐标;
,并分别写出点A1、B1、C1的坐标;
(3)求![]() 的面积.
的面积.
 0
0
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,∠ACB为锐角,点D为射线BC上一动点,连接AD,以AD为一边且在AD的右侧作正方形ADEF.解答下列问题:
(1)如果AB=AC,∠BAC=90°
①当点D在线段BC上时(与点B不重合),如图2,线段CF、BD之间的位置关系为 , 数量关系为 .
②当点D在线段BC的延长线上时,如图3,①中的结论是否仍然成立,为什么?
(2)如图4,如果AB≠AC,∠BAC≠90°,点D在线段BC上运动.且AC=4 ![]() ,BC=3,∠BCA=45°,正方形ADEF的边DE与线段CF相交于点P,求线段CP长的最大值.
,BC=3,∠BCA=45°,正方形ADEF的边DE与线段CF相交于点P,求线段CP长的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=![]() 在第一象限的图象经过点B,则△OAC与△BAD的面积之差S△OAC﹣S△BAD为( )
在第一象限的图象经过点B,则△OAC与△BAD的面积之差S△OAC﹣S△BAD为( )

A. 36 B. 12 C. 6 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是小颖往表姐家打长途电话的收费记录:
通话时间x(分钟) | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
电话费y(元) | 3 | 3 | 3 | 3.6 | 4.2 | 4.8 | 5.4 |
(1)上表的两个变量中, 是自变量, 是因变量;
(2)写出y与x之间的关系式;
(3)若小颖的通话时间是15分钟,则需要付多少电话费?
(4)若小颖有24元钱,则她最多能打多少分钟电话?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,正方形ABCD的边长为2,点M是BC的中点,P是线段MC上的一个动点(不与M、C重合),以AB为直径作⊙O,过点P作⊙O的切线,交AD于点F,切点为E.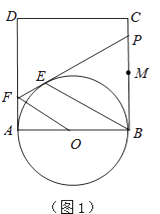
(1)求证:OF∥BE;
(2)设BP=x,AF=y,求y关于x的函数解析式,并写出自变量x的取值范围;
(3)延长DC、FP交于点G,连接OE并延长交直线DC于H(图2),问是否存在点P,使△EFO∽△EHG(E、F、O与E、H、G为对应点)?如果存在,试求(2)中x和y的值;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是⊙O的内接四边形,∠ABC=2∠D,连接OA、OB、OC、AC,OB与AC相交于点E,若∠COB=3∠AOB,OC=2 ![]() ,则图中阴影部分面积是(结果保留π和根号)
,则图中阴影部分面积是(结果保留π和根号)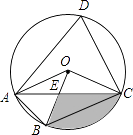
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小刚为调查某校七年级学生对某一节目的了解程度,用简单随机抽样的办法抽取了该年级的一个班进行调查统计.A:熟悉,B:了解较多,C:一般了解.图1和图2是他采集数据后,绘制的两幅不完整的统计图,请你根据图中提供的信息解答以下问题:
(1)求该班共有多少名学生.
(2)在条形图中,将表示“一般了解”的部分补充完整.
(3)如果全年级共400名同学,请你估算全年级对这一节目“了解较多”的学生人数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com