解:(1)∵抛物线y=-x
2+bx+c经过点A(-1,0),C(0,3),
∴

,
解得
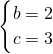
,
∴y=-x
2+2x+3,
令y=0,则-x
2+2x+3=0,
解得x
1=-1,x
2=3,
∴点B的坐标为(3,0),
设直线BC的解析式为y=kx+b,
则

,
解得
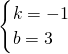
,
所以,直线BC的解析式为y=-x+3,
过点D作BC的平行直线,设解析式为y=-x+d,
联立

,
消掉y得,-x
2+2x+3=-x+d,
整理得,x
2-3x-3+d=0,
当△=0时,方程有两个相等的实数根,此时点D到BC的距离最大,△BDC的面积最大,
所以,x=-
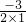
=

,
∵PD∥y轴,
∴点P的横坐标为

,
此时y=-

+3=

,
∴点P的坐标为(

,

);
(2)∵y=-x
2+2x+3=-(x-1)
2+4,
∴抛物线顶点E的坐标为(1,4),
过点C作CG⊥EF,则CG=1,
①点N在EG上时,点N与点E重合时,点M的横坐标最大,
∵点C(0,3),E(1,4),
∴GE=1,
∴∠CEG=45°,

∵∠MNC=90°,
∴∠MEF=90°-45°=45°,
∴MF=EF=4,
∴OM=4+1=5,
∴点M的坐标为(5,0),
即m的最大值为5,
②点N在线段GF上时,设GN=x,则NF=3-x,
∵∠MNC=90°,
∴∠CNG+∠MNF=90°,
又∵∠CNG+∠NCG=90°,
∴∠NCG=∠MNF,
∴Rt△NCG∽△MNF,
∴
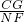
=
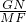
,
即
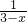
=
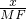
,
整理得,MF=-x
2+3x=-(x-

)
2+

,
所以,当x=

时,MF有最大值

,
MO=MF-OF=

-1=

,
所以,点M的坐标为(-

,0),
所以,m的最小值为-

,
因此,实数m的变化范围为-

≤m≤5.
故答案为:(

,

);-

≤m≤5.
分析:(1)把点A、C的坐标代入抛物线解析式求出b、c的值,从而得到抛物线的解析式,再求出点B的坐标,然后利用待定系数法求出直线BC的解析式,当与BC平行的直线与抛物线有且只有一个交点时,点D到BC的距离最大,此时△BDC的面积最大,然后联立直线与抛物线解析式,消掉y得到关于x的一元二次方程,利用根与系数的关系求出x的值,即可得到点D的横坐标,然后代入直线BC的解析式求出点P的纵坐标,即可得解;
(2)根据抛物线解析式求出顶点E的坐标,过点C作CG⊥%EF,然后分①点N在EG上时,点N与点E重合时,点M的横坐标最大,然后根据点C、E的坐标求出∠CEG=45°,再求出∠MEF=45°,根据等腰直角三角形的性质求出EM的长度,从而得到点M的坐标,求出m的最大值;②点N在线段GF上时,设GN=x,然后表示出NF,根据同角的余角相等求出∠NCG=∠MNF,然后证明△NCG和△MNF相似,根据相似三角形对应边成比例列出比例式用x表示出MF,再根据二次函数的最值问题求出y的最大值,然后求出MO,从而得到点M的坐标,求出m的最小值.
点评:本题是二次函数综合题型,主要考查了待定系数法求函数解析式(二次函数解析式与直线解析式),联立两函数解析式求交点坐标,平行直线的解析式的k值相等,相似三角形对应边成比例的性质,二次函数的最大值问题,综合性较强,难度较大,(2)要分情况讨论.

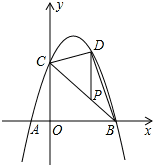 抛物线y=-x2+bx+c经过点A、B、C,已知A(-1,0),C(0,3).
抛物线y=-x2+bx+c经过点A、B、C,已知A(-1,0),C(0,3). ,
,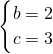 ,
, ,
,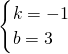 ,
, ,
,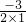 =
= ,
, ,
, +3=
+3= ,
, ,
, );
);
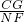 =
=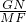 ,
,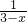 =
=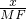 ,
, )2+
)2+ ,
, 时,MF有最大值
时,MF有最大值 ,
, -1=
-1= ,
, ,0),
,0), ,
, ≤m≤5.
≤m≤5. ,
, );-
);- ≤m≤5.
≤m≤5.

 名师点拨卷系列答案
名师点拨卷系列答案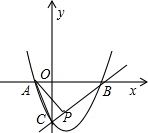 A是抛物线与x轴的另一个交点.
A是抛物线与x轴的另一个交点.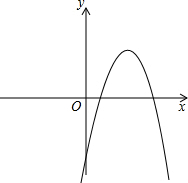 已知一元二次方程-x2+bx+c=0的两个实数根是m,4,其中0<m<4.
已知一元二次方程-x2+bx+c=0的两个实数根是m,4,其中0<m<4.