
【题目】如图,P为正方形ABCD的边BC上一动点(P与B、C不重合),连接AP,过点B作BQ⊥AP交CD于点Q,将△BQC沿BQ所在的直线对折得到△BQC′,延长QC′交BA的延长线于点M.
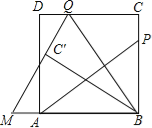
(1)试探究AP与BQ的数量关系,并证明你的结论;
(2)当AB=3,BP=2PC,求QM的长;
(3)当BP=m,PC=n时,求AM的长.
【答案】(1)AP=BQ,理由参见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)要证AP=BQ,只需证△PBA≌△QCB即可;
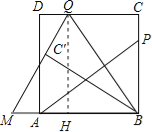
(2)过点Q作QH⊥AB于H,如图.易得QH=BC=AB=3,BP=2,PC=1,然后运用勾股定理可求得AP(即BQ)=![]() ,BH=2.易得DC∥AB,从而有∠CQB=∠QBA.由折叠可得∠C′QB=∠CQB,即可得到∠QBA=∠C′QB,即可得到MQ=MB.设QM=x,则有MB=x,MH=x﹣2.在Rt△MHQ中运用勾股定理就可解决问题;
,BH=2.易得DC∥AB,从而有∠CQB=∠QBA.由折叠可得∠C′QB=∠CQB,即可得到∠QBA=∠C′QB,即可得到MQ=MB.设QM=x,则有MB=x,MH=x﹣2.在Rt△MHQ中运用勾股定理就可解决问题;
(3)过点Q作QH⊥AB于H,如图,同(2)的方法求出QM的长,就可得到AM的长.
解:(1)AP=BQ.
理由:∵四边形ABCD是正方形,
∴AB=BC,∠ABC=∠C=90°,
∴∠ABQ+∠CBQ=90°.
∵BQ⊥AP,∴∠PAB+∠QBA=90°,
∴∠PAB=∠CBQ.
在△PBA和△QCB中,
 ,
,
∴△PBA≌△QCB,
∴AP=BQ;
(2)过点Q作QH⊥AB于H,如图.
∵四边形ABCD是正方形,
∴QH=BC=AB=3.
∵BP=2PC,
∴BP=2,PC=1,
∴BQ=AP=![]() =
=![]() =
=![]() ,
,
∴BH=![]() =
=![]() =2.
=2.
∵四边形ABCD是正方形,
∴DC∥AB,
∴∠CQB=∠QBA.
由折叠可得∠C′QB=∠CQB,
∴∠QBA=∠C′QB,
∴MQ=MB.
设QM=x,则有MB=x,MH=x﹣2.
在Rt△MHQ中,
根据勾股定理可得x2=(x﹣2)2+32,
解得x=![]() .
.
∴QM的长为![]() ;
;
(3)过点Q作QH⊥AB于H,如图.
∵四边形ABCD是正方形,BP=m,PC=n,
∴QH=BC=AB=m+n.
∴BQ2=AP2=AB2+PB2,
∴BH2=BQ2﹣QH2=AB2+PB2﹣AB2=PB2,
∴BH=PB=m.
设QM=x,则有MB=QM=x,MH=x﹣m.
在Rt△MHQ中,
根据勾股定理可得x2=(x﹣m)2+(m+n)2,
解得x=m+n+![]() ,
,
∴AM=MB﹣AB=m+n+![]() ﹣m﹣n=
﹣m﹣n=![]() .
.
∴AM的长为![]() .
.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】2016年某市用于资助贫困学生的助学金总额是9680000元,将9680000用科学记数法表示为( )
A. 96.8×105 B. 9.68×106 C. 9.68×107 D. 0.968×108
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形网格中,△OBC的顶点分别为O(0,0),B(3,﹣1)、C(2,1).
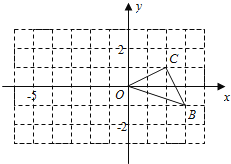
(1)以点O(0,0)为位似中心,按比例尺2:1在位似中心的异侧将△OBC放大为△OB′C′,放大后点B、C两点的对应点分别为B′、C′,画出△OB′C′,并写出点B′、C′的坐标:B′( , ),C′( , );
(2)在(1)中,若点M(x,y)为线段BC上任一点,写出变化后点M的对应点M′的坐标( , ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中错误的是( )
A. 掷一枚均匀的骰子,骰子停止转动后6点朝上是必然事件
B. 了解一批电视机的使用寿命,适合用抽样调查的方式
C. 若a为实数,则|a|<0是不可能事件
D. 甲、乙两人各进行10次射击,两人射击成绩的方差分别为S甲2=2,S乙2=4,则甲的射击成绩更稳定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我县七年级今年有4500名学生参加本次考试,要想了解这4500名学生的数学成绩从中抽取了500名考生的数学成绩进行统计分析,以下说法正确的是( )
A. 这500名考生是总体的一个样本 B. 每位考生是个体
C. 500名考生是总体 D. 这种调查是抽样调查
查看答案和解析>>
科目:初中数学 来源: 题型:
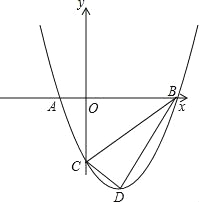
【题目】如图,抛物线与x轴交于A(﹣1,0)、B(3,0)两点,与y轴交于点C(0,﹣3),设抛物线的顶点为D.
(1)求该抛物线的解析式与顶点D的坐标;
(2)以B、C、D为顶点的三角形是直角三角形吗?为什么?
(3)探究坐标轴上是否存在点P,使得以P、A、C为顶点的三角形与△BCD相似?若存在,请指出符合条件的点P的位置,并直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com