
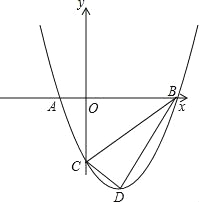
【题目】如图,抛物线与x轴交于A(﹣1,0)、B(3,0)两点,与y轴交于点C(0,﹣3),设抛物线的顶点为D.
(1)求该抛物线的解析式与顶点D的坐标;
(2)以B、C、D为顶点的三角形是直角三角形吗?为什么?
(3)探究坐标轴上是否存在点P,使得以P、A、C为顶点的三角形与△BCD相似?若存在,请指出符合条件的点P的位置,并直接写出点P的坐标;若不存在,请说明理由.
【答案】(1)顶点D的坐标为(1,﹣4).(2)△BCD为直角三角形.(3)符合条件的点有三个:O(0,0),![]() ,P2(9,0).
,P2(9,0).
【解析】
试题分析:(1)已知了抛物线图象上的三点坐标,可用待定系数法求出该抛物线的解析式,进而可用配方法或公式法求得顶点D的坐标.
(2)根据B、C、D的坐标,可求得△BCD三边的长,然后判断这三条边的长是否符合勾股定理即可.
(3)假设存在符合条件的P点;首先连接AC,根据A、C的坐标及(2)题所得△BDC三边的比例关系,即可判断出点O符合P点的要求,因此以P、A、C为顶点的三角形也必与△COA相似,那么分别过A、C作线段AC的垂线,这两条垂线与坐标轴的交点也符合点P点要求,可根据相似三角形的性质(或射影定理)求得OP的长,也就得到了点P的坐标.
试题解析:(1)设该抛物线的解析式为y=ax2+bx+c,
由抛物线与y轴交于点C(0,﹣3),可知c=﹣3,
即抛物线的解析式为y=ax2+bx﹣3,
把A(﹣1,0)、B(3,0)代入,
得![]()
解得a=1,b=﹣2.
∴抛物线的解析式为y=x2﹣2x﹣3,
∴顶点D的坐标为(1,﹣4).
(2)以B、C、D为顶点的三角形是直角三角形,
理由如下:
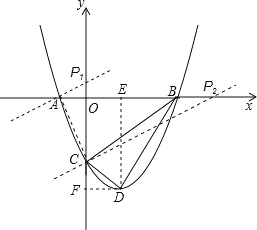
过点D分别作x轴、y轴的垂线,垂足分别为E、F.
在Rt△BOC中,OB=3,OC=3,
∴BC2=18,
在Rt△CDF中,DF=1,CF=OF﹣OC=4﹣3=1,
∴CD2=2,
在Rt△BDE中,DE=4,BE=OB﹣OE=3﹣1=2,
∴BD2=20,
∴BC2+CD2=BD2,故△BCD为直角三角形.
(3)连接AC,则容易得出△COA∽△CAP,又△PCA∽△BCD,可知Rt△COA∽Rt△BCD,得符合条件的点为O(0,0).
过A作AP1⊥AC交y轴正半轴于P1,可知Rt△CAP1∽Rt△COA∽Rt△BCD,
求得符合条件的点为![]() .
.
过C作CP2⊥AC交x轴正半轴于P2,可知Rt△P2CA∽Rt△COA∽Rt△BCD,
求得符合条件的点为P2(9,0).
∴符合条件的点有三个:O(0,0),![]() ,P2(9,0).
,P2(9,0).


科目:初中数学 来源: 题型:
【题目】如图,P为正方形ABCD的边BC上一动点(P与B、C不重合),连接AP,过点B作BQ⊥AP交CD于点Q,将△BQC沿BQ所在的直线对折得到△BQC′,延长QC′交BA的延长线于点M.
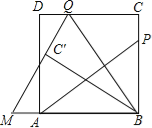
(1)试探究AP与BQ的数量关系,并证明你的结论;
(2)当AB=3,BP=2PC,求QM的长;
(3)当BP=m,PC=n时,求AM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(4分)在一个不透明的盒子里装有3个黑球和1个白球,每个球除颜色外都相同,从中任意摸出2个球,下列事件中,不可能事件是( )
A.摸出的2个球都是白球 B.摸出的2个球有一个是白球
C.摸出的2个球都是黑球 D.摸出的2个球有一个黑球
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列条件中,一定不能保证两直角三角形全等的是( )
A.两直角边对应相等B.一直角边与一锐角对应相等
C.两锐角对应相等D.斜边与一锐角对应相等
查看答案和解析>>
科目:初中数学 来源: 题型:
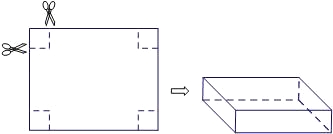
【题目】如图,把一张长15cm,宽12cm的矩形硬纸板的四周各剪去一个同样大小的小正方形,再折合成一个无盖的长方体盒子(纸板的厚度忽略不计).设剪去的小正方形的边长为xcm.
(1)请用含x的代数式表示长方体盒子的底面积;
(2)当剪去的小正方形的边长为多少时,其底面积是130cm2?
(3)试判断折合而成的长方体盒子的侧面积是否有最大值?若有,试求出最大值和此时剪去的小正方形的边长;若没有,试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A地的高度为3.72米.现在通过B,C两个中间点,最后测量远处的D地的高度,每次测量的结果如下表所示(单位:米):
B比A高 | C比B高 | D比C高 |
-1.44 | -3.62 | 7.16 |
则D地的高度是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com