
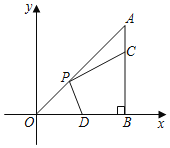
【题目】如图,在Rt△ABO中,∠OBA=90°,A(8,8),点C在边AB上,且![]() ,点D为OB的中点,点P为边OA上的动点,当点P在OA上移动时,使四边形PDBC周长最小的点P的坐标为( )
,点D为OB的中点,点P为边OA上的动点,当点P在OA上移动时,使四边形PDBC周长最小的点P的坐标为( )
A.(2,2)B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
根据已知条件得到AB=OB=8,∠AOB=45°,求得BC=6,OD=BD=4,得到D(4,0),C(8,6),作D关于直线OA的对称点E,连接EC交OA于P,则此时,四边形PDBC周长最小,E(0,4),求得直线EC的解析式为y=![]() x+4,解方程组即可得到结论.
x+4,解方程组即可得到结论.
解:∵在Rt△ABO中,∠OBA=90°,A(8,8),
∴AB=OB=8,∠AOB=45°,
∵![]() ,点D为OB的中点,
,点D为OB的中点,
∴BC=6,OD=BD=4,
∴D(4,0),C(8,6),
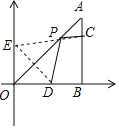
作D关于直线OA的对称点E,连接EC交OA于P,
则此时,四边形PDBC周长最小,E(0,4),
∵直线OA 的解析式为y=x,
设直线EC的解析式为y=kx+b,
∴![]() ,
,
解得:![]() ,
,
∴直线EC的解析式为y=![]() x+4,
x+4,
解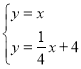 得,
得,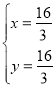 ,
,
∴P(![]() ,
,![]() ),
),
故选:D.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:
【题目】为了提高服务质量,某宾馆决定对甲、乙两种套房进行星级提升,已知甲种套房提升费用比乙种套房提升费用少3万元,如果提升相同数量的套房,甲种套房费用为625万元,乙种套房费用为700万元.
(1)甲、乙两种套房每套提升费用各多少万元?
(2)如果需要甲、乙两种套房共80套,市政府筹资金不少于2090万元,但不超过2096万元,且所筹资金全部用于甲、乙种套房星级提升,市政府对两种套房的提升有几种方案?哪一种方案的提升费用最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
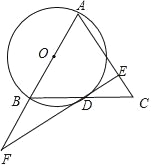
【题目】如图,在△ABC中,AB=AC,以AB为直径作⊙O交BC于点D,过点D作⊙O的切线DE交AC于点E,交AB延长线于点F.
(1)求证:BD=CD;
(2)求证:DC2=CEAC;
(3)当AC=5,BC=6时,求DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
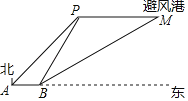
【题目】如图,一艘渔船正以60海里/小时的速度向正东方向航行,在A处测得岛礁P在东北方向上,继续航行1.5小时后到达B处,此时测得岛礁P在北偏东30°方向,同时测得岛礁P正东方向上的避风港M在北偏东60°方向.为了在台风到来之前用最短时间到达M处,渔船立刻加速以75海里/小时的速度继续航行_____小时即可到达.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,学校的实验楼对面是一幢教学楼,小敏在实验楼的窗口C测得教学楼顶部D的仰角为18°,教学楼底部B的俯角为20°,量得实验楼与教学楼之间的距离AB=30m.
(1)求∠BCD的度数.
(2)求教学楼的高BD.(结果精确到0.1m,参考数据:tan20°≈0.36,tan18°≈0.32)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,∠ACB=90°,OC=2BO,AC=6,点B的坐标为(1,0),抛物线y=﹣x2+bx+c经过A、B两点.
(1)求点A的坐标;
(2)求抛物线的解析式;
(3)点P是直线AB上方抛物线上的一点,过点P作PD垂直x轴于点D,交线段AB于点E,使PE=![]() DE.
DE.
①求点P的坐标;
②在直线PD上是否存在点M,使△ABM为直角三角形?若存在,求出符合条件的所有点M的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知顶点为A的抛物线y=a(x-![]() )2-2经过点B(-
)2-2经过点B(-![]() ,2),点C(
,2),点C(![]() ,2).
,2).
(1)求抛物线的表达式;
(2)如图1,直线AB与x轴相交于点M,与y轴相交于点E,抛物线与y轴相交于点F,在直线AB上有一点P,若∠OPM=∠MAF,求△POE的面积;
(3)如图2,点Q是折线A-B-C上一点,过点Q作QN∥y轴,过点E作EN∥x轴,直线QN与直线EN相交于点N,连接QE,将△QEN沿QE翻折得到△QEN′,若点N′落在x轴上,请直接写出Q点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已如:⊙O与⊙O上的一点A
(1)求作:⊙O的内接正六边形ABCDEF;( 要求:尺规作图,不写作法但保留作图痕迹)
(2)连接CE,BF,判断四边形BCEF是否为矩形,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com