
【题目】为了提高服务质量,某宾馆决定对甲、乙两种套房进行星级提升,已知甲种套房提升费用比乙种套房提升费用少3万元,如果提升相同数量的套房,甲种套房费用为625万元,乙种套房费用为700万元.
(1)甲、乙两种套房每套提升费用各多少万元?
(2)如果需要甲、乙两种套房共80套,市政府筹资金不少于2090万元,但不超过2096万元,且所筹资金全部用于甲、乙种套房星级提升,市政府对两种套房的提升有几种方案?哪一种方案的提升费用最少?
【答案】(1)甲、乙两种套房每套提升费用为25、28万元;(2)甲种套房提升50套,乙种套房提升30套时,y最小值为2090万元.
【解析】
(1)设甲种套房每套提升费用为x万元,根据题意建立方程求出其解即可;
(2)设甲种套房提升m套,那么乙种套房提升(80-m)套,根据条件建立不等式组求出其解就可以求出提升方案,再表示出总费用与m之间的函数关系式,根据一次函数的性质就可以求出结论.
(1)设乙种套房提升费用为x万元,则甲种套房提升费用为(x﹣3)万元,
则![]() ,
,
解得x=28.
经检验:x=28是分式方程的解,
答:甲、乙两种套房每套提升费用为25、28万元;
(2)设甲种套房提升a套,则乙种套房提升(80﹣a)套,
则2090≤25a+28(80﹣a)≤2096,
解得48≤a≤50.
∴共3种方案,分别为:
方案一:甲种套房提升48套,乙种套房提升32套.
方案二:甲种套房提升49套,乙种套房提升31套,
方案三:甲种套房提升50套,乙种套房提升30套.
设提升两种套房所需要的费用为y万元,则
y=25a+28(80﹣a)=﹣3a+2240,
∵k=﹣3,
∴当a取最大值50时,即方案三:甲种套房提升50套,乙种套房提升30套时,y最小值为2090万元.


科目:初中数学 来源: 题型:
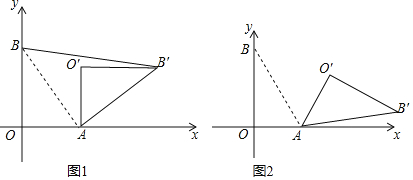
【题目】在平面直角坐标系中,O为原点,点A(3,0),点B(0,4),把△ABO绕点A顺时针旋转,得△AB′O′,点B,O旋转后的对应点为B′,O.
(1)如图1,当旋转角为90°时,求BB′的长;
(2)如图2,当旋转角为120°时,求点O′的坐标;
(3)在(2)的条件下,边OB上的一点P旋转后的对应点为P′,当O′P+AP′取得最小值时,求点P′的坐标.(直接写出结果即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,点A、B、C在x轴上,点D、E在y轴上,OA=OD=2,OC=OE=4,B为线段OA的中点,直线AD与经过B、E、C三点的抛物线交于F、G两点,与其对称轴交于M,点P为线段FG上一个动点(与F、G不重合),PQ∥y轴与抛物线交于点Q.
(1)求经过B、E、C三点的抛物线的解析式;
(2)判断△BDC的形状,并给出证明;当P在什么位置时,以P、O、C为顶点的三角形是等腰三角形,并求出此时点P的坐标;
(3)若抛物线的顶点为N,连接QN,探究四边形PMNQ的形状:①能否成为菱形;②能否成为等腰梯形?若能,请直接写出点P的坐标;若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
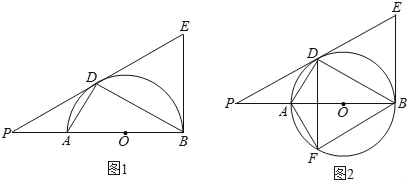
【题目】如图,AB是圆O的直径,O为圆心,AD、BD是半圆的弦,且∠PDA=∠PBD.延长PD交圆的切线BE于点E
(1)判断直线PD是否为⊙O的切线,并说明理由;
(2)如果∠BED=60°,PD=![]() ,求PA的长.
,求PA的长.
(3)将线段PD以直线AD为对称轴作对称线段DF,点F正好在圆O上,如图2,求证:四边形DFBE为菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
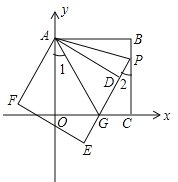
【题目】边长相等的两个正方形ABCO、ADEF如图摆放,正方形ABCO的边OA、OC在坐标轴上,ED交线段OC于点G,ED的延长线交线段BC于点P,连AG,已知OA长为![]() .
.
(1)求证:![]() ;
;
(2)若![]() ,AG=2,求点G的坐标;
,AG=2,求点G的坐标;
(3)在(2)条件下,在直线PE上找点M,使以M、A、G为顶点的三角形是等腰三角形,求出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
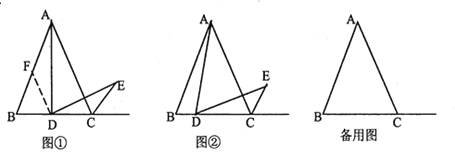
【题目】(1)(问题情境)小明遇到这样一个问题:
如图①,已知![]() 是等边三角形,点
是等边三角形,点![]() 为
为![]() 边上中点,
边上中点,![]() ,
,![]() 交等边三角形外角平分线
交等边三角形外角平分线![]() 所在的直线于点
所在的直线于点![]() ,试探究
,试探究![]() 与
与![]() 的数量关系.
的数量关系.
小明发现:过![]() 作
作![]() ,交
,交![]() 于
于![]() ,构造全等三角形,经推理论证问题得到解决.请直接写出
,构造全等三角形,经推理论证问题得到解决.请直接写出![]() 与
与![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
(2)(类比探究)
如图②,当![]() 是线段
是线段![]() 上(除
上(除![]() 外)任意一点时(其他条件不变)试猜想
外)任意一点时(其他条件不变)试猜想![]() 与
与![]() 的数量关系并证明你的结论.
的数量关系并证明你的结论.
(3)(拓展应用)
当![]() 是线段
是线段![]() 上延长线上,且满足
上延长线上,且满足![]() (其他条件不变)时,请判断
(其他条件不变)时,请判断![]() 的形状,并说明理由.
的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
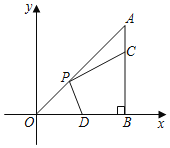
【题目】如图,在Rt△ABO中,∠OBA=90°,A(8,8),点C在边AB上,且![]() ,点D为OB的中点,点P为边OA上的动点,当点P在OA上移动时,使四边形PDBC周长最小的点P的坐标为( )
,点D为OB的中点,点P为边OA上的动点,当点P在OA上移动时,使四边形PDBC周长最小的点P的坐标为( )
A.(2,2)B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
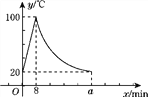
【题目】教师办公室有一种可以自动加热的饮水机,该饮水机的工作程序是:放满水后,接通电源,则自动开始加热,每分钟水温上升10 ℃,待加热到100 ℃,饮水机自动停止加热,水温开始下降,水温y(℃)和通电时间x(min)成反比例函数关系,直至水温降至室温,饮水机再次自动加热,重复上述过程.设某天水温和室温均为20 ℃,接通电源后,水温y(℃)和通电时间x(min)之间的关系如图所示,回答下列问题:
(1)分别求出当0≤x≤8和8<x≤a时,y和x之间的函数关系式;
(2)求出图中a的值;
(3)李老师这天早上7:30将饮水机电源打开,若他想在8:10上课前喝到不低于40 ℃的开水,则他需要在什么时间段内接水?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com