
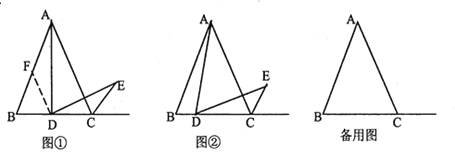
【题目】(1)(问题情境)小明遇到这样一个问题:
如图①,已知![]() 是等边三角形,点
是等边三角形,点![]() 为
为![]() 边上中点,
边上中点,![]() ,
,![]() 交等边三角形外角平分线
交等边三角形外角平分线![]() 所在的直线于点
所在的直线于点![]() ,试探究
,试探究![]() 与
与![]() 的数量关系.
的数量关系.
小明发现:过![]() 作
作![]() ,交
,交![]() 于
于![]() ,构造全等三角形,经推理论证问题得到解决.请直接写出
,构造全等三角形,经推理论证问题得到解决.请直接写出![]() 与
与![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
(2)(类比探究)
如图②,当![]() 是线段
是线段![]() 上(除
上(除![]() 外)任意一点时(其他条件不变)试猜想
外)任意一点时(其他条件不变)试猜想![]() 与
与![]() 的数量关系并证明你的结论.
的数量关系并证明你的结论.
(3)(拓展应用)
当![]() 是线段
是线段![]() 上延长线上,且满足
上延长线上,且满足![]() (其他条件不变)时,请判断
(其他条件不变)时,请判断![]() 的形状,并说明理由.
的形状,并说明理由.
【答案】(1)![]() ,理由见解析;(2)
,理由见解析;(2)![]() ,理由见解析;(3)
,理由见解析;(3)![]() 是等边三角形,理由见解析.
是等边三角形,理由见解析.
【解析】
(1)根据等边三角形的性质可得![]() ,然后根据平行线的性质可得
,然后根据平行线的性质可得![]() ,从而证出
,从而证出![]() 是等边三角形,即可证出
是等边三角形,即可证出![]() ,然后证出
,然后证出![]() 、
、![]() ,最后利用ASA即可证出
,最后利用ASA即可证出![]() ,从而得出结论;
,从而得出结论;
(2)过![]() 作
作![]() 交
交![]() 于
于![]() ,同理可知
,同理可知![]() 是等边三角形,从而证出
是等边三角形,从而证出![]() ,再证出
,再证出![]() 和
和![]() ,利用ASA即可证出
,利用ASA即可证出![]() ,从而得出结论;
,从而得出结论;
(3)根据等三角形的性质和已知条件可得![]() ,再根据三线合一可得
,再根据三线合一可得![]() 垂直平分
垂直平分![]() ,从而得出
,从而得出![]() ,再根据等边三角形的判定即可证出结论.
,再根据等边三角形的判定即可证出结论.
解:(1)![]() ,理由如下:
,理由如下:
∵![]() 是等边三角形,
是等边三角形,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() 是等边三角形,
是等边三角形,
∴![]() ,
,
又![]() ,
,
∴![]() ,
,
∵![]() 是
是![]() 外角平分线,
外角平分线,
∴![]() ,
,
∴![]() ,
,
∴![]()
∵![]() ,
,
∴![]() ,
,
∴在![]() 与
与![]() 中,
中,
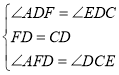
∴![]() ,
,
∴![]() ;
;
(2)![]()
证明:过![]() 作
作![]() 交
交![]() 于
于![]() ,
,
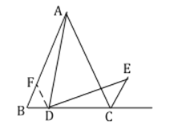
∵![]() 是等边三角形,
是等边三角形,
∴![]() 是等边三角形,
是等边三角形,
∴BF=BD
∴![]()
∵![]() ,
,![]() ,
,![]()
∴![]()
∵![]() 是
是![]() 外角平分线,
外角平分线,
∴![]() ,
,
∴![]() ,
,
∴![]()
在![]() 与
与![]() 中,
中,
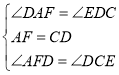
∴![]() ,
,
∴![]() ;
;
(3)![]() 是等边三角形,
是等边三角形,
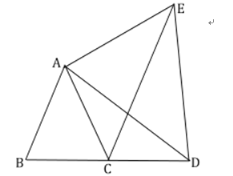
∵![]() 是等边三角形,
是等边三角形,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() 是等边三角形外角平分线.
是等边三角形外角平分线.
∴![]() 垂直平分
垂直平分![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() 是等边三角形.
是等边三角形.


科目:初中数学 来源: 题型:
【题目】如图,抛物线y= ![]() x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0).
x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0).
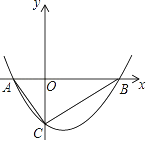
(1)求抛物线的解析式;
(2)判断△ABC的形状,证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,D是AB上的点,过点D作
,D是AB上的点,过点D作![]() 交BC于点F,交AC的延长线于点E,连接CD,
交BC于点F,交AC的延长线于点E,连接CD,![]() ,则下列结论正确的有( )
,则下列结论正确的有( )
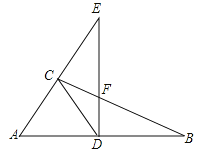
①∠DCB=∠B;②CD=![]() AB;③△ADC是等边三角形;④若∠E=30°,则DE=EF+CF.
AB;③△ADC是等边三角形;④若∠E=30°,则DE=EF+CF.
A. ①②③ B. ①②④ C. ②③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高服务质量,某宾馆决定对甲、乙两种套房进行星级提升,已知甲种套房提升费用比乙种套房提升费用少3万元,如果提升相同数量的套房,甲种套房费用为625万元,乙种套房费用为700万元.
(1)甲、乙两种套房每套提升费用各多少万元?
(2)如果需要甲、乙两种套房共80套,市政府筹资金不少于2090万元,但不超过2096万元,且所筹资金全部用于甲、乙种套房星级提升,市政府对两种套房的提升有几种方案?哪一种方案的提升费用最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,下列结论:①CD=ED;②AC+BE=AB;③∠BDE=∠BAC;④BE=DE;⑤SBDE:S△ACD=BD:AC,其中正确的个数( )
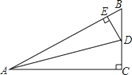
A.5个B.4个C.3个D.2个
查看答案和解析>>
科目:初中数学 来源: 题型:
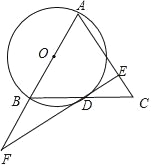
【题目】如图,在△ABC中,AB=AC,以AB为直径作⊙O交BC于点D,过点D作⊙O的切线DE交AC于点E,交AB延长线于点F.
(1)求证:BD=CD;
(2)求证:DC2=CEAC;
(3)当AC=5,BC=6时,求DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
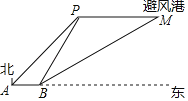
【题目】如图,一艘渔船正以60海里/小时的速度向正东方向航行,在A处测得岛礁P在东北方向上,继续航行1.5小时后到达B处,此时测得岛礁P在北偏东30°方向,同时测得岛礁P正东方向上的避风港M在北偏东60°方向.为了在台风到来之前用最短时间到达M处,渔船立刻加速以75海里/小时的速度继续航行_____小时即可到达.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,∠ACB=90°,OC=2BO,AC=6,点B的坐标为(1,0),抛物线y=﹣x2+bx+c经过A、B两点.
(1)求点A的坐标;
(2)求抛物线的解析式;
(3)点P是直线AB上方抛物线上的一点,过点P作PD垂直x轴于点D,交线段AB于点E,使PE=![]() DE.
DE.
①求点P的坐标;
②在直线PD上是否存在点M,使△ABM为直角三角形?若存在,求出符合条件的所有点M的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商家用1200元购进了一批T恤,上市后很快售完,商家又用2800元购进了第二批这种T恤,所购数量是第一批购进量的2倍,但单价贵了5元.
(1)该商家购进的第一批T恤是多少件?
(2)若两批T恤按相同的标价销售,最后剩下20件按八折优惠卖出,如果希望两批T恤全部售完的利润率不低于16%(不考虑其它因素),那么每件T恤的标价至少是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com