练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，抛物线y= x2+bx﹣2与x轴交于A、B两点，与y轴交于C点，且A（﹣1，0）．

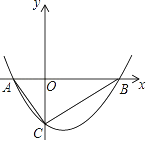
    （1）求抛物线的解析式；

    （2）判断△ABC的形状，证明你的结论．

    【答案】（1）y= x2﹣ x﹣2；（2）见解析

    【解析】试题分析：（1）因为点A在抛物线上，所以将点A代入函数解析式即可求得；

    （2）由函数解析式可以求得其与x轴、y轴的交点坐标，即可求得AB、BC、AC的长，由勾股定理的逆定理可得三角形的形状.

    试题解析：（1）∵点A（-1，0）在抛物线y=x2+bx-2上，

    ∴×（-1）2+b×（-1）-2=0，b=-

    ∴抛物线的解析式为y=x2-x-2

    （2）当x=0时y=-2，

    ∴C（0，-2），OC=2．

    当y=0时， x2-x-2=0，

    ∴x1=-1，x2=4，

    ∴B（4，0）．

    ∴OA=1，OB=4，AB=5．

    ∵AB2=25，AC2=OA2+OC2=5，BC2=OC2+OB2=20，

    ∴AC2+BC2=AB2．

    ∴△ABC是直角三角形．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

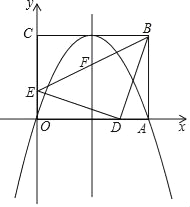
    【题目】如图，在平面直角坐标系中，矩形OABC的顶点A，C分别在x轴，y轴的正半轴上，且OA=4，OC=3，若抛物线经过O，A两点，且顶点在BC边上，对称轴交BE于点F，点D，E的坐标分别为（3，0），（0，1）．

    （1）求抛物线的解析式；

    （2）猜想△EDB的形状并加以证明；

    （3）点M在对称轴右侧的抛物线上，点N在x轴上，请问是否存在以点A，F，M，N为顶点的四边形是平行四边形？若存在，请求出所有符合条件的点M的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读下列材料，并完成相应的任务：

    杨辉三角

    我国著名数学家华罗庚曾在给青少年撰写的“数学是我国人民所擅长的学科”一文中谈到，我国古代数学的许多创新与发展都曾居世界前列，他说：“实际上我们祖国伟大人民在人类史上，有过无比睿智的成就．”其中“杨辉三角”就是一例．

    在我国南宋数学家杨辉（约13世纪）所著的《详解九章算术》（1261年）一书中，给出了二项式的展开式（按的次数由大到小的顺序排列）及其系数规律．

    如图所示

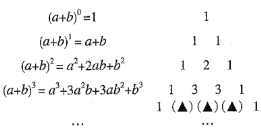
    任务：（1）通过观察，图中的（▲）中可填入的数字依次为______、______、______；

    （2）请直接写出的展开式：______；

    （3）根据（2）中的规律，求的值，写出计算过程．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

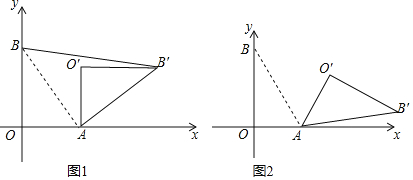
    【题目】在平面直角坐标系中，O为原点，点A（3，0），点B（0，4），把△ABO绕点A顺时针旋转，得△AB′O′，点B，O旋转后的对应点为B′，O．

    （1）如图1，当旋转角为90°时，求BB′的长；

    （2）如图2，当旋转角为120°时，求点O′的坐标；

    （3）在（2）的条件下，边OB上的一点P旋转后的对应点为P′，当O′P+AP′取得最小值时，求点P′的坐标．（直接写出结果即可）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知∠MON=，P为射线OM上的点，OP=1．

    （1）如图1，，A，B均为射线ON上的点，OA=1，OBOA，△PBC为等边三角形，且O，C两点位于直线PB的异侧，连接AC．

    ①依题意将图1补全；

    ②判断直线AC与OM的位置关系并加以证明；

    （2）若，Q为射线ON上一动点（Q与O不重合），以PQ为斜边作等腰直角△PQR，使O，R两点位于直线PQ的异侧，连接OR． 根据（1）的解答经验，直接写出△POR的面积．

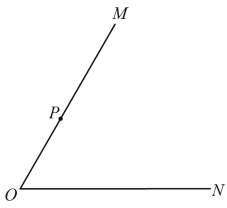
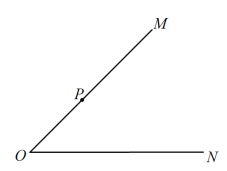
    图1 备用图

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】创新需要每个人的参与，就拿小华来说，为了解决晒衣服的，聪明的他想到了一个好办法，在家宽敞的院内地面上立两根等长的立柱、 (均与地面垂直),并在立柱之间悬挂一根绳子.由于挂的衣服比较多,绳子的形状近似成了抛物线,如图,已知立柱米, 米.

    （1）求绳子最低点离地面的距离;

    （2）为了防止衣服碰到地面,小华在离为米的位置处用一根垂直于地面的立柱撑起绳子 (如图2),使左边抛物线的最低点距为米,离地面米,求的长.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】图1，是一个长为，宽为的长方形，沿图中虚线用剪刀平均分成四块小长方形，然后按图2的形状拼成一个正方形．

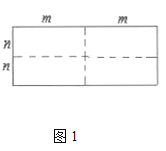
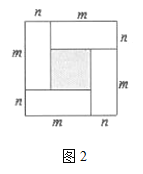
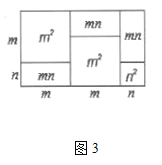
    （1）图2中的阴影部分的面积为 ；

    （2）观察图2，三个代数式，，之间的等量关系是 ；

    （3）若，，求；

    （4）观察图3，你能得到怎样的代数恒等式呢？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，平面直角坐标系中，点A、B、C在x轴上，点D、E在y轴上，OA=OD=2，OC=OE=4，B为线段OA的中点，直线AD与经过B、E、C三点的抛物线交于F、G两点，与其对称轴交于M，点P为线段FG上一个动点（与F、G不重合），PQ∥y轴与抛物线交于点Q．

    （1）求经过B、E、C三点的抛物线的解析式；

    （2）判断△BDC的形状，并给出证明；当P在什么位置时，以P、O、C为顶点的三角形是等腰三角形，并求出此时点P的坐标；

    （3）若抛物线的顶点为N，连接QN，探究四边形PMNQ的形状：①能否成为菱形；②能否成为等腰梯形？若能，请直接写出点P的坐标；若不能，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）（问题情境）小明遇到这样一个问题：

    如图①，已知是等边三角形，点为边上中点，，交等边三角形外角平分线所在的直线于点，试探究与的数量关系．

    小明发现：过作，交于，构造全等三角形，经推理论证问题得到解决．请直接写出与的数量关系，并说明理由．

    （2）（类比探究）

    如图②，当是线段上（除外）任意一点时（其他条件不变）试猜想与的数量关系并证明你的结论．

    （3）（拓展应用）

    当是线段上延长线上，且满足（其他条件不变）时，请判断的形状，并说明理由．

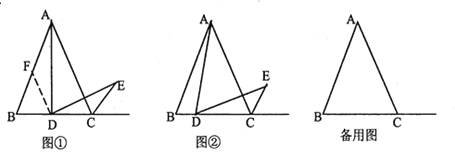
    查看答案和解析>>

    同步练习册答案