
【题目】边长相等的两个正方形ABCO、ADEF如图摆放,正方形ABCO的边OA、OC在坐标轴上,ED交线段OC于点G,ED的延长线交线段BC于点P,连AG,已知OA长为![]() .
.
(1)求证:![]() ;
;
(2)若![]() ,AG=2,求点G的坐标;
,AG=2,求点G的坐标;
(3)在(2)条件下,在直线PE上找点M,使以M、A、G为顶点的三角形是等腰三角形,求出点M的坐标.
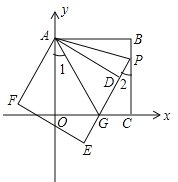
【答案】(1)证明见解析;(2)![]() ;(3)M坐标为
;(3)M坐标为![]() 或(
或(![]() .
.
【解析】
(1)由AO=AD,AG=AG,根据斜边和一条直角边对应相等的两个直角三角形全等,判断出![]() 即可;
即可;
(2)在![]() 中,由
中,由![]() ,
,![]() ,根据勾股定理求出OG的长,即可求出点G坐标;
,根据勾股定理求出OG的长,即可求出点G坐标;
(3)根据题意,分两种情况:①如图1,当点M在 y轴的负半轴上时;②如图2,当点M在GP延长线上时,作GH⊥AB于点H,通过全等三角形的性质及等边三角形的性质可得出点M为所求的点,再结合点A、点G的坐标即可求出点M的坐标.
(1)证明:在Rt△AOG和Rt△ADG中,![]()
∴△AOG≌△ADG(HL).
(2)解:∵在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,
∴G点坐标为![]() .
.
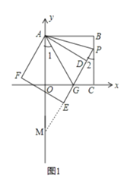
(3)①如图1,延长GE交![]() 轴于点M,
轴于点M,
∵△AOG≌△ADG,
∴![]() ,
,
又∵![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
在△AOG和△MOG中,
∴![]() ,
,
∴AG=MG,
∴△AGM为等腰三角形,
∵点A坐标为![]() ,
,
∴点M坐标为![]() .
.
②如图2,延长GP与AB的延长线交于点M,作GH⊥AB于点H.
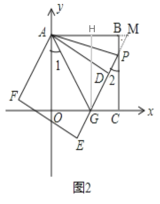
∵![]() ,
,
∴![]() ,
,
∴![]() ;
;
∴![]() ,
,
∴![]() 为等边三角形,
为等边三角形,
∴GH垂直平分线AM.
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴点M坐标为![]() .
.
综上可得点M坐标为![]() 或
或![]() .
.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
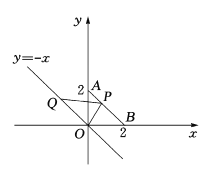
【题目】如图,在平面直角坐标系中,点![]() 的坐标是
的坐标是![]() ,点
,点![]() 的坐标是
的坐标是![]() ,连结
,连结![]() ,点
,点![]() 是线段
是线段![]() 上的一个动点(包括两端点),直线
上的一个动点(包括两端点),直线![]() 上有一动点
上有一动点![]() ,连结
,连结![]() ,已知
,已知![]() 的面积为
的面积为![]() ,则点
,则点![]() 的坐标为__________________.
的坐标为__________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正比例函数图象上一个点A到x轴的距离为4,点A的横坐标为-2,请回答下列问题:
(1)求这个正比例函数;
(2)这个正比例函数图象经过哪几个象限?
(3)这个正比例函数的函数值y是随着x的增大而增大?还是随着x的增大而减小?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高服务质量,某宾馆决定对甲、乙两种套房进行星级提升,已知甲种套房提升费用比乙种套房提升费用少3万元,如果提升相同数量的套房,甲种套房费用为625万元,乙种套房费用为700万元.
(1)甲、乙两种套房每套提升费用各多少万元?
(2)如果需要甲、乙两种套房共80套,市政府筹资金不少于2090万元,但不超过2096万元,且所筹资金全部用于甲、乙种套房星级提升,市政府对两种套房的提升有几种方案?哪一种方案的提升费用最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
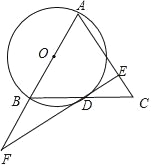
【题目】如图,在△ABC中,AB=AC,以AB为直径作⊙O交BC于点D,过点D作⊙O的切线DE交AC于点E,交AB延长线于点F.
(1)求证:BD=CD;
(2)求证:DC2=CEAC;
(3)当AC=5,BC=6时,求DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,学校的实验楼对面是一幢教学楼,小敏在实验楼的窗口C测得教学楼顶部D的仰角为18°,教学楼底部B的俯角为20°,量得实验楼与教学楼之间的距离AB=30m.
(1)求∠BCD的度数.
(2)求教学楼的高BD.(结果精确到0.1m,参考数据:tan20°≈0.36,tan18°≈0.32)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图1,OM是∠AOB的平分线,点C在OM上,OC=5,且点C到OA的距离为3.过点C作CD⊥OA,CE⊥OB,垂足分别为D、E,易得到结论:OD+OE=_________;

(1)把图1中的∠DCE绕点C旋转,当CD与OA不垂直时(如图2),上述结论是否成立?并说明理由;
(2)把图1中的∠DCE绕点C旋转,当CD与OA的反向延长线相交于点D时:
①请在图3中画出图形;
②上述结论还成立吗?若成立,请给出证明;若不成立,请直接写出线段OD、OE之间的数量关系,不需证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com