
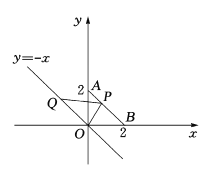
【题目】如图,在平面直角坐标系中,点![]() 的坐标是
的坐标是![]() ,点
,点![]() 的坐标是
的坐标是![]() ,连结
,连结![]() ,点
,点![]() 是线段
是线段![]() 上的一个动点(包括两端点),直线
上的一个动点(包括两端点),直线![]() 上有一动点
上有一动点![]() ,连结
,连结![]() ,已知
,已知![]() 的面积为
的面积为![]() ,则点
,则点![]() 的坐标为__________________.
的坐标为__________________.
【答案】![]() 或
或![]()
【解析】
由A、B点的坐标可得出直线AB的解析式,从而发现直线AB与直线OQ平行,由平行线间距离处处相等,可先求出点O到直线AB的距离,结合三角形面积公式求出线段OQ的长度,再依据两点间的距离公式可得出结论.
∵点Q在直线y=x上,
∴设点Q的坐标为(m,m).
∵点A的坐标是(0,2),点B的坐标是(2,0),
∴△AOB为等腰直角三角形,
点O(0,0)到AB的距离h=![]() OA=2.
OA=2.
设直线AB的解析式为y=kx+b,
∵点A(0,2),点B(2,0)在直线AB上,
∴有![]() ,解得
,解得![]() .
.
即直线AB的解析式为y=x+2,
∵直线y=x+2与y=x平行,
∴点P到底OQ的距离为![]() (平行线间距离处处相等).
(平行线间距离处处相等).
∵△OPQ的面积S△OPQ=![]() OQh=
OQh=![]() OQ=
OQ=![]() ,
,
∴OQ=2.
由两点间的距离公式可知OQ=![]() =2,
=2,
解得:m=±![]() ,
,
∴点Q的坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
故答案为:(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
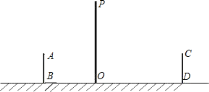
【题目】如图,是小亮晚上在广场散步的示意图,图中线段![]() 表示站立在广场上的小亮,线段
表示站立在广场上的小亮,线段![]() 表示直立在广场上的灯杆,点
表示直立在广场上的灯杆,点![]() 表示照明灯的位置.
表示照明灯的位置.
![]() 在小亮由
在小亮由![]() 处沿
处沿![]() 所在的方向行走到达
所在的方向行走到达![]() 处的过程中,他在地面上的影子长度越来越________(用“长”或“短”填空);请你在图中画出小亮站在
处的过程中,他在地面上的影子长度越来越________(用“长”或“短”填空);请你在图中画出小亮站在![]() 处的影子
处的影子![]() ;
;
![]() 当小亮离开灯杆的距离
当小亮离开灯杆的距离![]() 时,身高为
时,身高为![]() 的小亮的影长为
的小亮的影长为![]() ,
,
①灯杆的高度为多少![]() ?
?
②当小亮离开灯杆的距离![]() 时,小亮的影长变为多少
时,小亮的影长变为多少![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ACD是△ABC的外角,∠ABC的平分线与∠ACD的平分线交于点A1,∠A1BC的平分线与∠A1CD的平分线交于点A2,…,∠An﹣1BC的平分线与∠An﹣1CD的平分线交于点An.设∠A=θ.则:(1)∠A1=_____;(2)∠A2=_____;(3)∠An=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
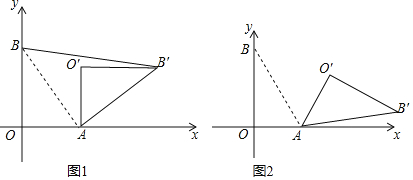
【题目】在平面直角坐标系中,O为原点,点A(3,0),点B(0,4),把△ABO绕点A顺时针旋转,得△AB′O′,点B,O旋转后的对应点为B′,O.
(1)如图1,当旋转角为90°时,求BB′的长;
(2)如图2,当旋转角为120°时,求点O′的坐标;
(3)在(2)的条件下,边OB上的一点P旋转后的对应点为P′,当O′P+AP′取得最小值时,求点P′的坐标.(直接写出结果即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】创新需要每个人的参与,就拿小华来说,为了解决晒衣服的,聪明的他想到了一个好办法,在家宽敞的院内地面![]() 上立两根等长的立柱
上立两根等长的立柱![]() 、
、![]() (均与地面垂直),并在立柱之间悬挂一根绳子.由于挂的衣服比较多,绳子的形状近似成了抛物线
(均与地面垂直),并在立柱之间悬挂一根绳子.由于挂的衣服比较多,绳子的形状近似成了抛物线![]() ,如图
,如图![]() ,已知立柱
,已知立柱![]() 米,
米, ![]() 米.
米.
(1)求绳子最低点离地面的距离;
(2)为了防止衣服碰到地面,小华在离![]() 为
为![]() 米的位置处用一根垂直于地面的立柱
米的位置处用一根垂直于地面的立柱![]() 撑起绳子 (如图2),使左边抛物线
撑起绳子 (如图2),使左边抛物线![]() 的最低点距
的最低点距![]() 为
为![]() 米,离地面
米,离地面![]() 米,求
米,求![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义[a,b,c]为函数y=ax2+bx+c的特征数,下面给出特征数为[2m,1﹣m,﹣1﹣m]的函数的一些结论,其中不正确的是( )
A. 当m=﹣3时,函数图象的顶点坐标是(![]() ,
,![]() )
)
B. 当m>0时,函数图象截x轴所得的线段长度大于![]()
C. 当m≠0时,函数图象经过同一个点
D. 当m<0时,函数在x>![]() 时,y随x的增大而减小
时,y随x的增大而减小
查看答案和解析>>
科目:初中数学 来源: 题型:
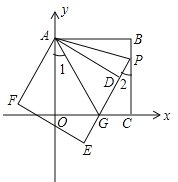
【题目】边长相等的两个正方形ABCO、ADEF如图摆放,正方形ABCO的边OA、OC在坐标轴上,ED交线段OC于点G,ED的延长线交线段BC于点P,连AG,已知OA长为![]() .
.
(1)求证:![]() ;
;
(2)若![]() ,AG=2,求点G的坐标;
,AG=2,求点G的坐标;
(3)在(2)条件下,在直线PE上找点M,使以M、A、G为顶点的三角形是等腰三角形,求出点M的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com