
【题目】如图,在△ABC中,∠C=∠ABC,BE⊥AC,垂足为点E,△BDE是等边三角形,若AD=4,则线段BE的长为______.

【答案】4
【解析】
本题首先由等边三角形的性质及垂直定义得到∠DBE=60°,∠BEC=90°,再根据等腰三角形的性质可以得出∠EBC=∠ABC-60°=∠C-60°,最后根据三角形内角和定理得出关系式∠C-60°+∠C=90°解出∠C,推出AD=DE,于是得到结论.
∵△BDE是正三角形,
∴∠DBE=60°;
∵在△ABC中,∠C=∠ABC,BE⊥AC,
∴∠C=∠ABC=∠ABE+∠EBC,则∠EBC=∠ABC-60°=∠C-60°,∠BEC=90°;
∴∠EBC+∠C=90°,即∠C-60°+∠C=90°,
解得∠C=75°,
∴∠ABC=75°,
∴∠A=30°,
∵∠AED=90°-∠DEB=30°,
∴∠A=∠AED,
∴DE=AD=4,
∴BE=DE=4,
故答案为:4.


科目:初中数学 来源: 题型:
【题目】家庭过期药品属于“国家危险废物“处理不当将污染环境,危害健康。某市药监部门为了了解市民家庭处理过期药品的方式,决定对全市家庭作一次简单随机抽样调查
(1)下列选取样本的方法最合理的一种是(只需填上正确答案的序号)
①在市中心某个居民区以家庭为单位随机抽取;
②在全市医务工作者中以家庭为单位随机抽取③在全市常住人口中以家庭为单位随机抽取.
(2)本次抽样调查发现,接受调查的家庭都有过期药品,现将有关数据呈现如下图: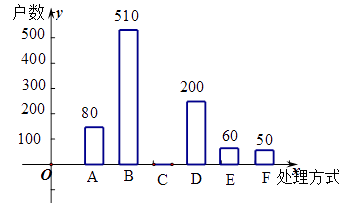
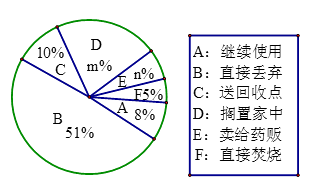
①求m、n的值.
②补全条形统计图
③根据调查数据,你认为该市市民家庭处理过期药品最常见的方式是什么?
④家庭过期药品的正确处理方式是送回收点,若该市有180万户家庭,请估计大约有多少户家庭处理过期药品的方式是送回收点。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,张老师举了下面的例题:
例 1 等腰三角形 ABC 中,∠A=110°,求∠B 的度数.
例 2 等腰三角形 ABC 中,∠A=40°,求∠B 的度数.
张老师启发同学们进行变式,小敏编了如下一题:变式等腰三角形 ABC 中,∠A=70°,求∠B 的度数.
(1)请你解答以上的变式题.
(2)在等腰三角形 ABC 中,设∠A=x°,请用 x°表示出∠B 的度数;
(3)结合(1)(2),小敏发现,∠A 的度数不同,得到∠B 的度数的个数也可能不同,当∠B 有三种情况三个不同的度数时,讨论此时 x 的取值范围
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解某校九年级学生的跳高水平,随机抽取该年级50名学生进行跳高测试,并把测试成绩绘制成如图所示的频数表和未完成的频数直方图(每组含前一个边界值,不含后一个边界值).
某校九年级50名学生跳高测试成绩的频数表
组别(m) | 频数 |
1.09~1.19 | 8 |
1.19~1.29 | 12 |
1.29~1.39 | A |
1.39~1.49 | 10 |
(1)求a的值,并把频数直方图补充完整;
(2)该年级共有500名学生,估计该年级学生跳高成绩在1.29m(含1.29m)以上的人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠B=30°,AD⊥AB,交BC于点D,AD=4,则BC的长为( )
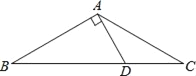
A. 8 B. 4 C. 12 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:二次函数y=ax2+bx的图象经过点M(1,n)、N(3,n).
(1)求b与a之间的关系式;
(2)若二次函数y=ax2+bx的图象与x轴交于点A、B,顶点为C,△ABC为直角三角形,求该二次函数的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数y=ax2+bx+c的图象经过点A(﹣1,0),B(0,﹣ ![]() ),C(2,0),其对称轴与x轴交于点D
),C(2,0),其对称轴与x轴交于点D
(1)求二次函数的表达式及其顶点坐标;
(2)若P为y轴上的一个动点,连接PD,则 ![]() PB+PD的最小值为;
PB+PD的最小值为;
(3)M(x,t)为抛物线对称轴上一动点
①若平面内存在点N,使得以A,B,M,N为顶点的四边形为菱形,则这样的点N共有 个;
②连接MA,MB,若∠AMB不小于60°,求t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某科技有限公司准备购进A和B两种机器人来搬运化工材料,已知购进A种机器人2个和B种机器人3个共需16万元,购进A种机器人3个和B种机器人2个共需14万元,请解答下列问题:
(1)求A、B两种机器人每个的进价;
(2)已知该公司购买B种机器人的个数比购买A种机器人的个数的2倍多4个,如果需要购买A、B两种机器人的总个数不少于28个,且该公司购买的A、B两种机器人的总费用不超过106万元,那么该公司有哪几种购买方案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com