
【题目】已知:二次函数y=ax2+bx的图象经过点M(1,n)、N(3,n).
(1)求b与a之间的关系式;
(2)若二次函数y=ax2+bx的图象与x轴交于点A、B,顶点为C,△ABC为直角三角形,求该二次函数的关系式.
【答案】
(1)解:∵图象经过M(1,n)、N(3,n),
∴图象的对称轴为直线x=2,
∴﹣ ![]() =2,所以b=﹣4a;
=2,所以b=﹣4a;
(2)解:y=ax2﹣4ax的图象与x轴交于点A(0,0)、B(4,0),
∵△ABC为直角三角形,
∴顶点C坐标为(2,2)或(2,﹣2),
代入得4a﹣8a=2或4a﹣8a=﹣2,
∴a=﹣ ![]() 或
或 ![]() ,
,
∴该二次函数的关系式为:y=﹣ ![]() x2+2x或y=
x2+2x或y= ![]() x2﹣2x.
x2﹣2x.
【解析】(1)直接利用二次函数对称性得出对称轴,进而得出答案;(2)利用等腰直角三角形的性质得出C点坐标,进而得出答案.
【考点精析】利用抛物线与坐标轴的交点对题目进行判断即可得到答案,需要熟知一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.


科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=3,AD=1,AB在数轴上,若以点A为圆心,对角线AC的长为半径作弧交数轴的正半轴于M,则点M的表示的数为________________.
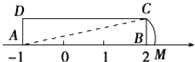
【答案】![]()
【解析】AC=AM=![]() =
=![]() ,∴AM=
,∴AM=![]()
【题型】填空题
【结束】
11
【题目】在△ABC中,AB=10,AC=2![]() ,BC边上的高AD=6,则另一边BC等于_______.
,BC边上的高AD=6,则另一边BC等于_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果商从批发市场用8000元购进了大樱桃和小樱桃各200千克,大樱桃的进价比小樱桃的进价每千克多20元.大樱桃售价为每千克40元,小樱桃售价为每千克16元.
(1)大樱桃和小樱桃的进价分别是每千克多少元?销售完后,该水果商共赚了多少元钱?
(2)该水果商第二次仍用8000元钱从批发市场购进了大樱桃和小樱桃各200千克,进价不变,但在运输过程中小樱桃损耗了20%.若小樱桃的售价不变,要想让第二次赚的钱不少于第一次所赚钱的90%,大樱桃的售价最少应为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,(1)已知∠ABC,射线ED∥AB,过点E作∠DEF=∠ABC,试说明BC∥EF;
(2)如图②,已知∠ABC,射线ED∥AB,∠ABC+∠DEF=180°.判断直线BC与直线EF的位置关系,并说明理由;
(3)根据以上探究,你发现了一个什么结论?请你写出来;
(4)如图③,已知AC⊥BC,CD⊥AB,DE⊥AC,HF⊥AB,若∠1=48°,试求∠2的度数.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,填空:
(1)若∠4=∠3,则____∥_____,理由是______;
(2)若∠2=∠E,则____∥___,理由是____;
(3)若∠A=∠ABE=180°,则____∥___,理由是____;
(4)若∠2=∠____,则DA∥EB,理由是____;
(5)若∠DBC+∠_____=180°,则DB∥EC,理由是____;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个全等的等腰直角三角板(斜边长为2)如图放置,其中一块三角板45°角的顶点与另一块三角板ABC的直角顶点A重合.若三角板ABC固定,当另一个三角板绕点A旋转时,它的直角边和斜边所在的直线分别与边BC交于点E、F.设BF=x,CE=y,则y关于x的函数图象大致是( )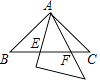
A.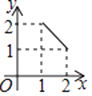
B.
C.
D.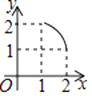
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,抛物线y=ax2+bx经过两点A(﹣1,1),B(2,2).过点B作BC∥x轴,交抛物线于点C,交y轴于点D.
(1)求此抛物线对应的函数表达式及点C的坐标;
(2)若抛物线上存在点M,使得△BCM的面积为 ![]() ,求出点M的坐标;
,求出点M的坐标;
(3)连接OA、OB、OC、AC,在坐标平面内,求使得△AOC与△OBN相似(边OA与边OB对应)的点N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,∠B=60°,△AB′C′可以由△ABC绕点A顺时针旋转90°得到(点B′与点B是对应点,点C′与点C是对应点),连接CC′,则∠CC′B′的度数是( ) 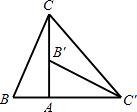
A.45°
B.30°
C.25°
D.15°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com