
����Ŀ����ѧ���ϣ�����ʦ������������⣺
�� 1 ���������� ABC �У���A��110�������B �Ķ�����
�� 2 ���������� ABC �У���A��40�������B �Ķ�����
����ʦ����ͬѧ�ǽ��б�ʽ��С����������һ�⣺��ʽ���������� ABC �У���A��70�������B �Ķ�����
��1�����������ϵı�ʽ�⣮
��2���ڵ��������� ABC �У����A��x�������� x����ʾ����B �Ķ�����
��3����ϣ�1����2����С�����֣���A �Ķ�����ͬ���õ���B �Ķ����ĸ���Ҳ���ܲ�ͬ������B ���������������ͬ�Ķ���ʱ�����۴�ʱ x ��ȡֵ��Χ
���𰸡�(1)������;(2)������;(3)������.
��������
��1�����������ηֱ���⼴�ɽ��������
��2�����������ηֱ���⼴�ɽ��������
��3��������������������������ʽ���ɽ��������
��1������AΪ���������B����180�㩁��A����2��55�㣻
����AΪ������BΪ���������B��180�㩁2��70�㣽40�㣻
����AΪ������BΪ�������B��70�㣻
���B��55���40���70�㣻
��2������AΪ���������B����![]() ���㣻
���㣻
����AΪ������BΪ���������B����180��2x���㣻
����AΪ������BΪ�������B��x�㣮
��3�������������
����90��x��180ʱ����Aֻ��Ϊ���������B�Ķ���ֻ��һ����������ȥ����
����0��x��90ʱ�����������
 ���ⲻ��ʽ�����x��60�㣮
���ⲻ��ʽ�����x��60�㣮
������������֪��0��x��90��x��60ʱ����B��������ͬ�Ķ�����


 ѧ���쳵�����ּ��ں�����ҵϵ�д�
ѧ���쳵�����ּ��ں�����ҵϵ�д� ��˼ά������ҵϵ�д�
��˼ά������ҵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ�β���У�ijͬѧվ�ڵ�A���۲�ͣ����B��C������С������ô�B�ڵ�A��ƫ��75������150�״�����C�ڵ�A��ƫ��15������120�״�����B�봬C֮��ľ���Ϊ______�ף���ȷ��0.1![]() ����
����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�����֪a+b����4��ab��3����a2+b2��ֵ��
�⣺��a+b����4��ab��3��
��a2+b2��(a+b)2��2ab��(��4)2��2��3��10��
���������������˼·����������⣺
(1)��֪a��b����3��ab����2����(a+b)(a2��b2)��ֵ��
(2)��֪a��c��b����10��(a��b)c����12����(a��b)2+c2��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(1)�Ȼ�������ֵ![]() x2��2(x��
x2��2(x��![]() y2)��
y2)��![]() (��3x2��2y2)��
(��3x2��2y2)��![]() x������x��2��y����3��
x������x��2��y����3��
(2)��֪A��2a2��a��B����5a��1.
������3A��2B��2��
����a����![]() ʱ����3A��2B��2��ֵ��
ʱ����3A��2B��2��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����E��F�ֱ���AB��CD�ϵĵ㣬��G��BC���ӳ�����һ�㣬�ҡ�B����DCG����D���������ж��У��������(�� ��)

A. ��AEF����EFC B. ��A����BCF C. ��AEF����EBC D. ��BEF����EFC��180��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijˮ���̴������г���8000Ԫ�����˴�ӣ�Һ�Сӣ�Ҹ�200ǧ�ˣ���ӣ�ҵĽ��۱�Сӣ�ҵĽ���ÿǧ�˶�20Ԫ.��ӣ���ۼ�Ϊÿǧ��40Ԫ��Сӣ���ۼ�Ϊÿǧ��16Ԫ.
(1)��ӣ�Һ�Сӣ�ҵĽ��۷ֱ���ÿǧ�˶���Ԫ?�������ˮ���̹��˶���ԪǮ?
(2)��ˮ���̵ڶ�������8000ԪǮ�������г������˴�ӣ�Һ�Сӣ�Ҹ�200ǧ�ˣ����۲��䣬�������������Сӣ�������20%����Сӣ�ҵ��ۼ۲��䣬Ҫ���õڶ�����Ǯ�����ڵ�һ����Ǯ��90%����ӣ�ҵ��ۼ�����ӦΪ���٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
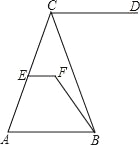
����Ŀ����ͼ��CD��AB����DCB=70�㣬��CBF=20�㣬��EFB=130�㣬
��1����ֱ��EF��AB��������λ�ù�ϵ������֤����
��2������CEF=70�������ACB�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���C����ABC��BE��AC������Ϊ��E����BDE�ǵȱ������Σ���AD��4�����߶�BE�ij�Ϊ______��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������˵������������������ޣ��������ޡ������ޡ�ŷ��Լռ�������50%���۷���Լռȫ�������![]() �������������Լ�Ǵ����������2����������ȷ��˵����( )
�������������Լ�Ǵ����������2����������ȷ��˵����( )
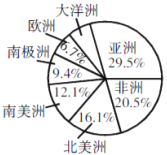
A. �٢� B. �٢ڢۢ� C. �٢� D. �٢ۢ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com