
分析 (1)根据甲、乙两同学从家到学校的距离之比是10:7,甲同学的家与学校的距离为3000米,即可求出乙同学的家与学校的距离;
(2)设乙骑自行车的速度为x米/分,则公交车的速度是2x米/分,根据甲乙两同学同时从家发去学校,结果甲同学比乙同学早到2分钟列方程即可得到结论.
解答 解:(1)∵甲、乙两同学从家到学校的距离之比是10:7,甲同学的家与学校的距离为3000米,
∴乙同学的家与学校的距离=3000×$\frac{7}{10}$=2100(米).
答:乙同学的家与学校的距离为2100米;
(2)设乙骑自行车的速度为x米/分,则公交车的速度为2x米/分.
依题意得:$\frac{2100}{x}$-$\frac{3000}{2x}$=2,
解得:x=300,
经检验,x=300是方程的根.
答:乙骑自行车的速度为300米/分.
点评 此题主要考查了分式方程的应用,分析题意,找到合适的等量关系是解决问题的关键.


科目:初中数学 来源: 题型:解答题
 阅读对学生的成长有着深远的影响,某中学为了解学生每周课余阅读的时间,在本校随机抽取了若干名学生进行调查,并依据调查结果绘制了以下不完整的统计图表.
阅读对学生的成长有着深远的影响,某中学为了解学生每周课余阅读的时间,在本校随机抽取了若干名学生进行调查,并依据调查结果绘制了以下不完整的统计图表.| 组别 | 时间(小时) | 频数(人数) | 频率 |
| A | 0≤t≤0.5 | 6 | 0.15 |
| B | 0.5≤t≤1 | a | 0.3 |
| C | 1≤t≤1.5 | 10 | 0.25 |
| D | 1.5≤t≤2 | 8 | b |
| E | 2≤t≤2.5 | 4 | 0.1 |
| 合计 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,正方形ABCD中,AB=6,点E在边CD上,且CE=2DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③EG=DE+BG;④AG∥CF;⑤S△FGC=3.6.其中正确结论是①②③④⑤.
如图,正方形ABCD中,AB=6,点E在边CD上,且CE=2DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③EG=DE+BG;④AG∥CF;⑤S△FGC=3.6.其中正确结论是①②③④⑤.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
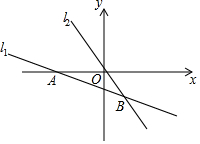 如图,在平面直角坐标系中,直线l1:y=-$\frac{1}{2}$x+b与直线l2:y=kx相交于点B(m,-4),且直线l1与x轴交于点A(-6,0).
如图,在平面直角坐标系中,直线l1:y=-$\frac{1}{2}$x+b与直线l2:y=kx相交于点B(m,-4),且直线l1与x轴交于点A(-6,0).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
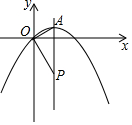 已知:如图,在平面直角坐标系中,抛物线y=ax2+x的对称轴为直线x=2,顶点为A.点P为抛物线对称轴上一点,连结OA、OP.当OA⊥OP时,P点坐标为(2,-4).
已知:如图,在平面直角坐标系中,抛物线y=ax2+x的对称轴为直线x=2,顶点为A.点P为抛物线对称轴上一点,连结OA、OP.当OA⊥OP时,P点坐标为(2,-4).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
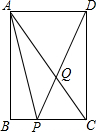 如图,矩形ABCD中,AB=4,AD=3,点Q在对角线AC上,且AQ=AD,连接DQ并延长,与边BC交于点P,则线段AP=$\sqrt{17}$.
如图,矩形ABCD中,AB=4,AD=3,点Q在对角线AC上,且AQ=AD,连接DQ并延长,与边BC交于点P,则线段AP=$\sqrt{17}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com