
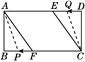
����Ŀ����֪���ھ���ABCD�У�AB��4 cm��BC��8 cm��AC�Ĵ�ֱƽ����EF�ֱ�AD��BC�ڵ�E��F������ΪO.
(1)��ͼ�٣�����AF��CE����˵���ı���AFCEΪ���Σ�����AF�ij���
(2)��ͼ�ڣ�����P��Q�ֱ��A��C����ͬʱ�������ء�AFB�͡�CDE���������˶�һ�ܣ�����P��A��F��B��Aֹͣ����Q��C��D��E��Cֹͣ�����˶������У���֪��P���ٶ�Ϊ5 cm/s����Q���ٶ�Ϊ4 cm/s���˶�ʱ��Ϊt s������A��C��P��Q�ĵ�Ϊ������ı�����ƽ���ı���ʱ����t��ֵ��

���𰸡���1��AF��5 cm����2��t��![]() .
.
�������������������1��������֪������֤OA��OC��OE��OF�����ݶԽ�����ƽ�ֵ��ı�����ƽ���ı��������ж��ı���AFCEΪƽ���ı���������EF��AC�����ݶԽ����ഹֱ��ƽ���ı���Ϊ���Σ������ж��ı���AFCEΪ��������AF��CF��x cm����BF��(8��x)cm����Rt��ABF�У����ݹ��ɶ����г����̣��ⷽ�����x��ֵ���������AF�ij�����2����P����AF�ϣ�Q����CD��ʱ��A��C��P��Q�ĵ㲻���ܹ���ƽ���ı��Σ�ͬ��P����AB�ϣ�Q����DE��CE��ʱ��Ҳ�����ܹ���ƽ���ı��Σ����ֻ�е�P����BF�ϣ�Q����ED��ʱ�����ܹ���ƽ���ı��Σ���ͼ������AP��CQ������A��C��P��Q�ĵ�Ϊ������ı�����ƽ���ı��Σ���ʱPC��QA����t��ʾ��PC��QA�ij����г�������t����.
���������
(1)���ı���ABCD�Ǿ��Σ�
��AD��BC.
���CAD����ACB����AEF����CFE.
��EF��ֱƽ��AC������ΪO��
��OA��OC.
���AOE�ա�COF.
��OE��OF.
���ı���AFCEΪƽ���ı��Σ�
����EF��AC��
���ı���AFCEΪ���Σ�
��AF��CF��x cm����BF��(8��x)cm��
��Rt��ABF�У�AB��4 cm���ɹ��ɶ�����42��(8��x)2��x2�����x��5.
��AF��5 cm.
(2)��Ȼ��P����AF�ϣ�Q����CD��ʱ��A��C��P��Q�ĵ㲻���ܹ���ƽ���ı��Σ�ͬ��P����AB�ϣ�Q����DE��CE��ʱ��Ҳ�����ܹ���ƽ���ı��Σ����ֻ�е�P����BF�ϣ�Q����ED��ʱ�����ܹ���ƽ���ı��Σ���ͼ������AP��CQ������A��C��P��Q�ĵ�Ϊ������ı�����ƽ���ı��Σ���ʱPC��QA.����P���ٶ�Ϊ5 cm/s����Q���ٶ�Ϊ4 cm/s���˶�ʱ��Ϊt s��
��PC��5t cm��QA��(12��4t)cm.��5t��12��4t�����t��![]() .
.
����A��C��P��Q�ĵ�Ϊ������ı�����ƽ���ı���ʱ��t��![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
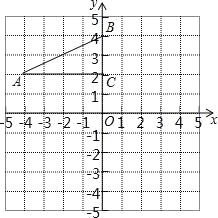
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�Rt��ABC����������ֱ���A����4��2����B��0��4����C��0��2����
��1��������ABC���ڵ�C�����ĶԳƵ���A1B1C��ƽ����ABC������A�Ķ�Ӧ��A2������Ϊ��0����4��������ƽ�ƺ��Ӧ����A2B2C2��
��2����A1B1C����A2B2C2����ijһ������ĶԳƣ���Գ����ĵ�����Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������߶��У��ܳɱ������ǣ�������
A. 3cm��6cm��8cm��9cmB. 3cm��5cm��6cm��9cm
C. 3cm��6cm��7cm��9cmD. 3cm��6cm��9cm��18cm
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪A��x2+ax��B��2bx2��4x��1���Ҷ���ʽ2A+B��ֵ����ĸx��ȡֵ�أ���a��b��ֵ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵����ȷ���ǣ� ��
A. ��ԭ���ֱ�߶������������� B. ����������ͼ��ԭ��
C. y=kx������������ D. y=3+x������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����P�ĺ�������3���ҵ�x��ľ���Ϊ5�����P��������______________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�˶�Ʒ�Ƶ�Ե�һ����A��B�����˶�Ь�������������ͳ�ƣ������˶�Ь���������������۶���ͼ��ʾ��
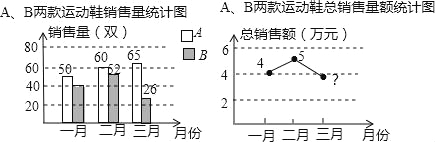
��1��һ�·�B���˶�Ь����������A���![]() ����һ�·�B���˶�Ь�����˶���˫��
����һ�·�B���˶�Ь�����˶���˫��
��2����һ�����������˶�Ь�����۵��۱��ֲ��䣬�����·ݵ������۶���۶�=���۵���������������
��3���ۺϵ�һ���ȵ����������������������˶�Ь�Ľ��������۵ȷ������һ�����飮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����йز���ͳ�ƣ�2018������һС�������ڼ䣬�㶫���㹲�Ӵ��ο�Լ14420000�˴Σ�����14420000�ÿ�ѧ��������ʾΪ��������
A. 1.442��107 B. 0.1442��107 C. 1.442��108 D. 0.1442��108
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com