
分析 (1)先计算乘方、负整数指数幂、三角函数及绝对值,再计算乘法,最后计算加减法即可得;
(2)根据分式的混合运算顺序和法则化简原式,再由非负数的性质得出x、y的值,代入计算即可得.
解答 解:(1)原式=-4-3+2×$\frac{\sqrt{3}}{2}$-($\sqrt{3}$-1)
=-7+$\sqrt{3}$-$\sqrt{3}$+1
=-6;
(2)原式=1-$\frac{x-y}{x+2y}$•$\frac{(x+2y)^{2}}{(x+y)(x-y)}$
=$\frac{x+y}{x+y}$-$\frac{x+2y}{x+y}$
=-$\frac{y}{x+y}$,
由|x-2|+(2x-y-3)2=0知x=2,2x-y-3=0,
则y=1,
∴当x=2、y=1时,原式=-$\frac{1}{2+1}$=-$\frac{1}{3}$.
点评 本题考查了实数的混合运算、分式的化简求值.解题的关键是对分式的分子分母要因式分解.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
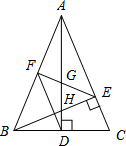 如图,在△ABC中,AB=AC,AD和BE是高,∠ABE=45°,点F是AB的中点,AD与FE、BE分别交于点G、H.有下列结论:①FD=FE;②AH=2CD;③BC•AD=$\sqrt{2}$AE2;④S△ABC=4S△ADF.其中正确结论的序号是①②③④.(把你认为正确结论的序号都填上).
如图,在△ABC中,AB=AC,AD和BE是高,∠ABE=45°,点F是AB的中点,AD与FE、BE分别交于点G、H.有下列结论:①FD=FE;②AH=2CD;③BC•AD=$\sqrt{2}$AE2;④S△ABC=4S△ADF.其中正确结论的序号是①②③④.(把你认为正确结论的序号都填上).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 国家旅游局调查国民对“五一”期间出行旅游的满意程度 | |
| B. | 调查中国民众对美国在韩部署萨德系统持反对态度的比例 | |
| C. | 调查中国国产航母各零部件的质量 | |
| D. | 调查重庆市初2017级学生的中考体考成绩 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
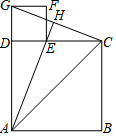 如图,已知四边形ABCD和四边形DEFG为正方形,点E在线段DC上,点A、D、G在同一直线上,且AD=3,DE=1,连接AC、CG、AE,并延长AE交OG于点H.
如图,已知四边形ABCD和四边形DEFG为正方形,点E在线段DC上,点A、D、G在同一直线上,且AD=3,DE=1,连接AC、CG、AE,并延长AE交OG于点H.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com