
【题目】某动物园成人票每张20元,学生票每张5元,国庆期间特推出以下两种优惠方案:
方案一:购买一张成人票赠送一张学生票;
方法二:按总价的90%付款.
某校有4名教师带领若干名(不少于4人)学生去参观该动物园.
(1)设学生人数为x(人),付款总金额y(元),分别建立两种优惠方案中y与x的函数关系式;
(2)请计算并确定出比较节省费用的购票方案.
【答案】(1)![]() ;
;![]() ;(2)当学生人数为 24人时,两种优惠方案付款一样多;当学生人数大于等于4人少于 24人时,方案1比较节省费用;当学生人数大于24人时,方案2比较节省费用.
;(2)当学生人数为 24人时,两种优惠方案付款一样多;当学生人数大于等于4人少于 24人时,方案1比较节省费用;当学生人数大于24人时,方案2比较节省费用.
【解析】分析:(1)首先根据优惠方案①:付款总金额=购买成人票金额+除去4人后的学生票金额;
优惠方案②:付款总金额=(购买成人票金额+购买学生票金额)×打折率,列出y关于x的函数关系式,
(2)根据(1)的函数关系式求出当两种方案付款总金额相等时,购买的票数.再就三种情况讨论.
详解:(1)按优惠方案①可得
y1=20×4+(x-4)×5=5x+60(x≥4),
按优惠方案②可得
y2=(5x+20×4)×90%=4.5x+72(x≥4);
(2)因为y1-y2=0.5x-12(x≥4),
①当y1-y2=0时,得0.5x-12=0,解得x=24,
∴当购买24张票时,两种优惠方案付款一样多.
②当y1-y2<0时,得0.5x-12<0,解得x<24,
∴4≤x<24时,y1<y2,优惠方案①付款较少.
③当y1-y2>0时,得0.5x-12>0,解得x>24,
当x>24时,y1>y2,优惠方案②付款较少.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:
【题目】骰子是6个面上分别写有数字1,2,3,4,5,6的小立方体,它任意两对面上所写的两个数字之和为7.将这样相同的几个骰子按照相接触的两个面上的数字的积为6摆成一个几何体,这个几何体的三视图如图所示.已知图中所标注的是部分面上的数字,则“*”所代表的数是( )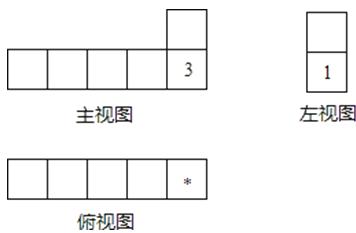
A.2
B.4
C.5
D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学兴趣小组想测量河流的宽度AB,河流两岸AC,BD互相平行,河流对岸有两棵树A和C,且A、C之间的距离是60m,他们在D处测得∠BDC=36°,前行140米后测得∠BPA=45°,请根据这些数据求出河流的宽度.
(结果精确到0.1米,参考数据:tan36°≈0.73,sin36°≈0.59,cos36°≈0.81)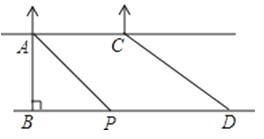
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一张矩形ABCD纸片按如图方式折叠,使点A与点E重合,点C与点F重合(E、F两点均在BD上),折痕分别为BH、DG. 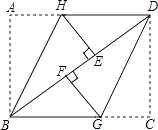
(1)求证:△BHE≌△DGF;
(2)若AB=6cm,BC=8cm,求线段FG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】蜗牛从某点![]() 开始沿一东西方向直线爬行,规定向东爬行的路程记为正数,向西爬行的路程记为负数.爬过的各段路程依次为(单位:厘米):
开始沿一东西方向直线爬行,规定向东爬行的路程记为正数,向西爬行的路程记为负数.爬过的各段路程依次为(单位:厘米):![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() 通过计算说明蜗牛是否回到起点
通过计算说明蜗牛是否回到起点![]() .
.
![]() 蜗牛离开出发点
蜗牛离开出发点![]() 最远时是多少厘米?
最远时是多少厘米?
![]() 在爬行过程中,如果每爬
在爬行过程中,如果每爬![]() 厘米奖励
厘米奖励![]() 粒芝麻,则蜗牛一共得到多少粒芝麻?
粒芝麻,则蜗牛一共得到多少粒芝麻?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近两年,国际市场黄金价格涨幅较大,中国交通银行推出“沃德金”的理财产品,即以黄金为投资产品,投资者从黄金价格的上涨中赚取利润.上周五黄金的收盘价为285元/克,下表是本周星期一至星期五黄金价格的变化情况.(注:星期一至星期五开市,星期六.星期日休市)
星期 | 一 | 二 | 三 | 四 | 五 |
收盘价的变化(与前一天收盘价比较) | +7 | +5 |
|
| +8 |
问:(1)本周星期三黄金的收盘价是多少?
(2)本周黄金收盘时的最高价.最低价分别是多少?
(3)上周,小王以周五的收盘价285元/克买入黄金1000克,已知买入与卖出时均需支付成交金额的千分之五的交易费,卖出黄金时需支付成交金额的千分之三的印花税.本周,小王以周五的收盘价全部卖出黄金1000克,他的收益情况如何?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a、b、c满足|a﹣![]() |+
|+![]() +(c﹣4
+(c﹣4![]() )2=0.
)2=0.
(1)求a、b、c的值;
(2)判断以a、b、c为边能否构成三角形?若能构成三角形,此三角形是什么形状?并求出三角形的面积;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索规律,观察下面算式,解答问题.
1+3 =4 =22;
1+3+5=9=32;
1+3+5+7=16=42;
1+3+5+7+9=25=52;
(1)请猜想1+3+5+7+9+…+19=
(2)请猜想1+3+5+7+9+…+(2n-1)+(2n +1)+(2n +3)=
(3)试计算:101 +103+…+197 +199.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD,BE.
(1)求证:CE=AD;
(2)当D为AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com