
分析 此题首先由题意得出等量关系,即A型机器人搬运900kg与B型机器人搬运600kg所用时间相等,列出方程为$\frac{900}{x+30}$=$\frac{600}{x}$,从而解出方程,最后检验并作答.
解答 解:设B型机器人每小时搬运xkg,则A型机器人每小时搬运(x+30)kg.
依题意列方程得:$\frac{900}{x+30}$=$\frac{600}{x}$,
解得:x=60.
经检验x=60是原方程的根且符合题意.
当x=60时,x+30=90.
答:A型机器人每小时搬运90kg,B型机器人每小时搬运60kg.
点评 本题主要考查分式方程的应用,解题的关键是熟练掌握列分式方程解应用题的一般步骤,即①根据题意找出等量关系,②列出方程,③解出分式方程,④检验,⑤作答.注意:分式方程的解必须检验.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
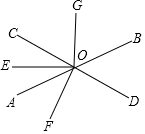 如图,直线AB与CD相交于O,OE是∠AOC的平分线,OF⊥CD,OG⊥OE,∠BOD=52°.
如图,直线AB与CD相交于O,OE是∠AOC的平分线,OF⊥CD,OG⊥OE,∠BOD=52°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
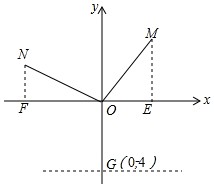 如图,在直角坐标系中,已知点M(2,3),连接OM,在第二象限作N,使ON⊥OM且ON=OM,y轴上有一点G(0,-4),过G作x轴的平行线l.
如图,在直角坐标系中,已知点M(2,3),连接OM,在第二象限作N,使ON⊥OM且ON=OM,y轴上有一点G(0,-4),过G作x轴的平行线l.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
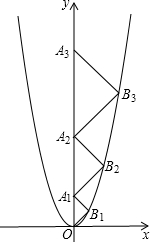 如图,在平面直角坐标系xOy中,点A1,A2,A3,…,An在y轴的正半轴上,点B1,B2,B3,…,Bn在二次函数y=x2位于第一象限的图象上,若△OB1A1,△A1B2A2,△A2B3A3,…,△An-1BnAn都是等腰直角三角形,其中∠B1=∠B2=∠B3=…=∠Bn=90°,则:
如图,在平面直角坐标系xOy中,点A1,A2,A3,…,An在y轴的正半轴上,点B1,B2,B3,…,Bn在二次函数y=x2位于第一象限的图象上,若△OB1A1,△A1B2A2,△A2B3A3,…,△An-1BnAn都是等腰直角三角形,其中∠B1=∠B2=∠B3=…=∠Bn=90°,则:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m<2 | B. | m>2 | C. | m≤2 | D. | m≥2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com