
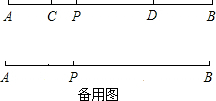
 如图,P是定长线段AB上一点,C、D两点同时从P、B出发分别以1cm/s和2cm/s的速度沿直线AB向左运动(C在线段AP上,D在线段BP上).已知C、D运动到任一时刻时,总有PD=2AC.
如图,P是定长线段AB上一点,C、D两点同时从P、B出发分别以1cm/s和2cm/s的速度沿直线AB向左运动(C在线段AP上,D在线段BP上).已知C、D运动到任一时刻时,总有PD=2AC.| 1 |
| 2 |
| MN |
| AB |
| MN |
| AB |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
 解:(1)根据C、D的运动速度知:BD=2PC,
解:(1)根据C、D的运动速度知:BD=2PC,| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| MN |
| AB |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| MN |
| AB |
| 1 |
| 12 |


科目:初中数学 来源: 题型:

| PQ |
| AB |

| 1 |
| 2 |
| MN |
| AB |

查看答案和解析>>
科目:初中数学 来源: 题型:
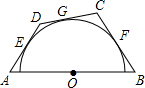 如图,AB是定长线段,圆心O是AB的中点,AE、BF为切线,E、F为切点,满足AE=BF,在
如图,AB是定长线段,圆心O是AB的中点,AE、BF为切线,E、F为切点,满足AE=BF,在 |
| EF |
| A、正比例函数y=kx(k为常数,k≠0,x>0) | ||
| B、一次函数y=kx+b(k,b为常数,kb≠0,x>0) | ||
C、反比例函数y=
| ||
| D、二次函数y=ax2+bx+c(a,b,c为常数,a≠0,x>0) |
查看答案和解析>>
科目:初中数学 来源:江西省期末题 题型:解答题

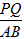 的值。
的值。 
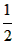 AB,此时C点停止运动,D点继续运动(D点在线段PB上),M、N分别是CD、PD的中点,下列结论:①PM-PN的值不变;②
AB,此时C点停止运动,D点继续运动(D点在线段PB上),M、N分别是CD、PD的中点,下列结论:①PM-PN的值不变;② 的值不变,可以说明,只有一个结论是正确的,请你找出正确的结论并求值。
的值不变,可以说明,只有一个结论是正确的,请你找出正确的结论并求值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com