
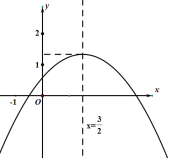
【题目】如图所示,抛物线y=ax2+bx+c的对称轴为x=![]() ,与x轴的一个交点A(
,与x轴的一个交点A(![]() ,0),抛物线的顶点B纵坐标1<yB<2,则以下结论:①abc<0;②b2-4ac>0;③3a-b=0;④4a+c<0;⑤
,0),抛物线的顶点B纵坐标1<yB<2,则以下结论:①abc<0;②b2-4ac>0;③3a-b=0;④4a+c<0;⑤![]() <a<
<a<![]() .其中正确结论的个数是( )
.其中正确结论的个数是( )
A. 2 B. 3 C. 4 D. 5
【答案】B
【解析】
由抛物线开口方向,对称轴的位置以及与![]() 轴的交点位置,确定
轴的交点位置,确定![]() 的正负,由抛物线与x轴有两个交点得到b2-4ac>0;抛物线y=ax2+bx+c的对称轴为x=
的正负,由抛物线与x轴有两个交点得到b2-4ac>0;抛物线y=ax2+bx+c的对称轴为x=![]() ,即可判断③;抛物线与x轴的一个交点A(
,即可判断③;抛物线与x轴的一个交点A(![]() ,0),得到
,0),得到![]() 把把b=3a代入即可判断④,根据抛物线的顶点B纵坐标1<yB<2,即可判断⑤.
把把b=3a代入即可判断④,根据抛物线的顶点B纵坐标1<yB<2,即可判断⑤.
①∵抛物线开口向下,
∴a<0,
∵对称轴是:![]() ,
,
∴a、b异号,
∴b>0,
∵抛物线与y轴交于正半轴,
∴c>0,
∴abc<0,
∴选项①正确;
②∵抛物线与x轴有两个交点,
∴b2-4ac>0
选项②正确;
③抛物线对称轴是:![]()
b=3a,
3a+b=0,
∴选项③不正确;
④抛物线与x轴的一个交点A(![]() ,0),
,0),
![]()
把b=3a代入得:![]()
![]()
故选项④正确;
⑤由对称性得:抛物线与x轴的另一个交点为![]()
抛物线的方程为:![]()
抛物线的顶点B纵坐标1<yB<2,
![]()
解得:![]()
∴选项⑤不正确;
正确的有3个,
故选:B


科目:初中数学 来源: 题型:
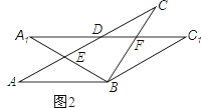
【题目】在△ABC中,AB=BC=2,∠ABC=120°,将△ABC绕点B顺时针旋转角α(0°<α<90°)得△A1BC1,A1B交AC于点E,A1C1分别交AC、BC于D、F两点.
(1)如图1,观察并猜想,在旋转过程中,线段BE与BF有怎样的数量关系?并证明你的结论;
(2)如图2,当α=30°时,试判断四边形BC1DA的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
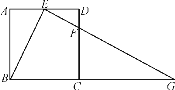
【题目】如图,在正方形ABCD中,E、F分别是边AD、CD上的点,AE=ED,DF=![]() DC,连接EF并延长交BC的延长线于点G.
DC,连接EF并延长交BC的延长线于点G.
(1)求证:△ABE∽△DEF;
(2)若正方形的边长为4,求BG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
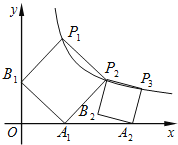
【题目】正方形的A1B1P1P2顶点P1、P2在反比例函数y=![]() (x>0)的图象上,顶点A1、B1分别在x轴、y轴的正半轴上,再在其右侧作正方形P2P3A2B2,顶点P3在反比例函数y=
(x>0)的图象上,顶点A1、B1分别在x轴、y轴的正半轴上,再在其右侧作正方形P2P3A2B2,顶点P3在反比例函数y=![]() (x>0)的图象上,顶点A2在x轴的正半轴上,则点P3的坐标为 .
(x>0)的图象上,顶点A2在x轴的正半轴上,则点P3的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
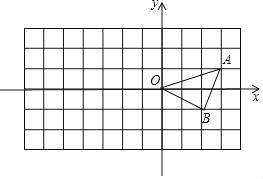
【题目】方格纸中每个小正方形的边长都是单位1,△OAB在平面直角坐标系中的位置如图所示.解答问题:
(1)请按要求对△ABO作如下变换:
①将△OAB向下平移2个单位,再向左平移3个单位得到△O1A1B1;
②以点O为位似中心,位似比为2:1,将△ABC在位似中心的异侧进行放大得到△OA2B2.
(2)写出点A1,A2的坐标: , ;
(3)△OA2B2的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,并解决问题:任意一个大于1的正整数m都可以表示为:m=p2+q(p、q是正整数),在m的所有这种表示中,如果![]() 最小时,规定:F(m)=
最小时,规定:F(m)=![]() .例如:21可以表示为:21=12+20=22+17=32+12=42+5,因为
.例如:21可以表示为:21=12+20=22+17=32+12=42+5,因为![]() >
>![]() >
>![]() >
>![]() ,所以F(21)=
,所以F(21)=![]() .
.
(1)求F(33)的值;
(2)如果一个正整数n可以表示为t2-t(其中t≥2,且是正整数),那么称n是次完全平方数,证明:任何一个次完全平方数n,都有F(n)=1;
(3)一个三位自然数k,k=100a+10b+c(其中1≤a≤9,0≤b≤9,0≤c≤9,且a≤c,a、b、c为整数),满足十位上的数字恰好等于百位上的数字与个位上的数字之和,且k与其十位上数字的2倍之和能被9整除,求所有满足条件的k中F(k)的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC,DE∥BC,点F在边AC上,DF与BE相交于点G,且∠EDF=∠ABE.

求证:(1)△DEF∽△BDE;(2)DGDF=DBEF.
查看答案和解析>>
科目:初中数学 来源: 题型:
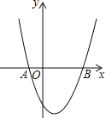
【题目】如图,已知抛物线y=x2+bx+c经过A(﹣1,0)、B(3,0)两点.
(1)求抛物线的解析式和顶点坐标;
(2)点P为抛物线上一点,若S△PAB=10,求出此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周末,小凯和同学带着皮尺,去测量杨大爷家露台遮阳篷的宽度.如图,由于无法直接测量,小凯便在楼前地面上选择了一条直线EF,通过在直线EF上选点观测,发现当他位于N点时,他的视线从M点通过露台D点正好落在遮阳篷A点处;当他位于N′点时,视线从M′点通过D点正好落在遮阳篷B点处,这样观测到的两个点A、B间的距离即为遮阳篷的宽.已知AB∥CD∥EF,点C在AG上,AG、DE、MN、M′N′均垂直于EF,MN=M′N′,露台的宽CD=GE.实际测得,GE=5米,EN=15.5米,NN′=6.2米.请根据以上信息,求出遮阳篷的宽AB是多少米?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com