
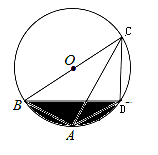
【题目】如图,四边形ABCD内接于⊙O,BC是直径,∠BAD=120°,AB=AD.
(1)、求证:四边形ABCD是等腰梯形;(2)、已知AC=6,求阴影部分的面积.
【答案】(1)、证明过程见解析(2)、4π-3![]()
【解析】
试题分析:(1)根据AB=AD,∠BAD=120°可以得到∠ABD=∠ADB=30°,从而说明弧AB和弧AD的度数为60°,根据BC为直径可以说明弧CD的度数也是60°,从而可以得到AB=CD,然后根据∠CAD=∠ACB=30°得出AD∥BC;(2)、阴影部分面积利用扇形面积减去△BOD的面积.
试题解析:⑴、∵∠BAD=120°,AB=AD ∴∠ABD=∠ADB=30° ∴弧AB和弧AD的度数都等于60°
又 ∵BC是直径 ∴弧CD的度数也是60°∴AB=CD
∵∠CAD=∠ACB=30°∴BC∥AD ∴四边形ABCD是等腰梯形.
⑵、∵BC是直径 ∴∠BAC=90° ∵∠ACB=30°,AC=6∴BC=![]() ∴r=2
∴r=2![]()
∵弧AB和弧AD的度数都等于60°∴∠BOD=120°
连接OA交BD于点E,则OA⊥BD ∴OE=OB×sin30°=![]() BE=0B×cos30°=3BD=2BE=6
BE=0B×cos30°=3BD=2BE=6
∴![]() =
=![]() =4π-3
=4π-3![]() .
.


 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+2交x轴于A(﹣1,0),B(4,0)两点,交y轴于点C,与过点C且平行于x轴的直线交于另一点D,点P是抛物线上一动点.
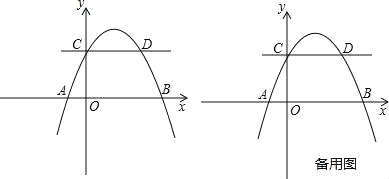
(1)求抛物线解析式及点D坐标;
(2)点E在x轴上,若以A,E,D,P为顶点的四边形是平行四边形,求此时点P的坐标;
(3)过点P作直线CD的垂线,垂足为Q,若将△CPQ沿CP翻折,点Q的对应点为Q′.是否存在点P,使Q′恰好落在x轴上?若存在,求出此时点P的坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com