
،¾جâؤ؟،؟بçح¼£¬إ×خïدكy=ax2+bx+2½»xضلسعA£¨©پ1£¬0£©£¬B£¨4£¬0£©ء½µم£¬½»yضلسعµمC£¬سë¹µمCازئ½ذذسعxضلµؤض±دك½»سعءيز»µمD£¬µمPتاإ×خïدكةدز»¶¯µم£®
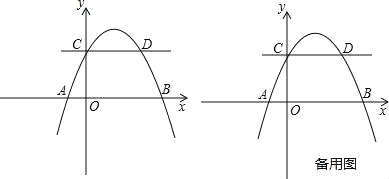
£¨1£©اَإ×خïدك½âخِت½¼°µمD×ّ±ê£»
£¨2£©µمEشعxضلةد£¬بôزشA£¬E£¬D£¬Pخھ¶¥µمµؤثؤ±كذختائ½ذذثؤ±كذخ£¬اَ´ثت±µمPµؤ×ّ±ê£»
£¨3£©¹µمP×÷ض±دكCDµؤ´¹دك£¬´¹×مخھQ£¬بô½«،÷CPQرطCP·صغ£¬µمQµؤ¶شس¦µمخھQ،ن£®تا·ٌ´وشعµمP£¬ت¹Q،نا،؛أآنشعxضلةد£؟بô´وشع£¬اَ³ِ´ثت±µمPµؤ×ّ±ê£»بô²»´وشع£¬ثµأ÷ہيسة£®
،¾´ً°¸،؟(1)،¢y=©پ![]() x2+
x2+![]() x+2£»D(3£¬2)£»(2)،¢P1£¨0£¬2£©£»P2£¨
x+2£»D(3£¬2)£»(2)،¢P1£¨0£¬2£©£»P2£¨![]() £¬©پ2£©£»P3£¨
£¬©پ2£©£»P3£¨![]() £¬©پ2£©£»(3)،¢£¨
£¬©پ2£©£»(3)،¢£¨![]() £¬
£¬![]() £©£¬£¨©پ
£©£¬£¨©پ![]() £¬
£¬![]() £©
£©
،¾½âخِ،؟
تشجâ·ضخِ£؛(1)،¢سأ´¶¨دµت·¨؟ةµأ³ِإ×خïدكµؤ½âخِت½£¬ءîy=2؟ةµأ³ِµمDµؤ×ّ±ê£»(2)،¢·ضء½ضضاé؟ِ½ّذذجضآغ£¬¢ظµ±AEخھز»±كت±£¬AE،خPD£¬¢عµ±AEخھ¶ش½ادكت±£¬¸ù¾فئ½ذذثؤ±كذخ¶ش¶¥µمµ½ءيز»جُ¶ش½ادك¾àہëدàµب£¬اَ½âµمP×ّ±ê£»(3)،¢½ل؛دح¼ذخ؟ةإذ¶د³ِµمPشعض±دكCDدآ·½£¬ةèµمPµؤ×ّ±êخھ£¨a£¬©پ![]() a2+
a2+![]() a+2£©£¬·ضاé؟ِجضآغ£¬¢ظµ±Pµمشعyضلسز²àت±£¬¢عµ±Pµمشعyضل×َ²àت±£¬شثسأ½âض±½اب½اذخ¼°دàثئب½اذخµؤذشضت½ّذذاَ½â¼´؟ة£®
a+2£©£¬·ضاé؟ِجضآغ£¬¢ظµ±Pµمشعyضلسز²àت±£¬¢عµ±Pµمشعyضل×َ²àت±£¬شثسأ½âض±½اب½اذخ¼°دàثئب½اذخµؤذشضت½ّذذاَ½â¼´؟ة£®
تشجâ½âخِ£؛(1)،¢،كإ×خïدكy=ax2+bx+2¾¹A£¨©پ1£¬0£©£¬B£¨4£¬0£©ء½µم£¬،à![]() £¬
£¬
½âµأ£؛ ،ày=©پ
،ày=©پ![]() x2+
x2+![]() x+2£»µ±y=2ت±£¬©پ
x+2£»µ±y=2ت±£¬©پ![]() x2+
x2+![]() x+2=2£¬½âµأ£؛x1=3£¬x2=0£¨ةلب¥£©£¬
x+2=2£¬½âµأ£؛x1=3£¬x2=0£¨ةلب¥£©£¬
¼´£؛µمD×ّ±êخھ£¨3£¬2£©£®
(2)،¢A£¬Eء½µم¶¼شعxضلةد£¬AEسذء½ضض؟ةؤـ£؛
¢ظµ±AEخھز»±كت±£¬AE،خPD£¬ ،àP1£¨0£¬2£©£¬
¢عµ±AEخھ¶ش½ادكت±£¬¸ù¾فئ½ذذثؤ±كذخ¶ش¶¥µمµ½ءيز»جُ¶ش½ادك¾àہëدàµب£¬
؟ةضھPµم،¢Dµمµ½ض±دكAE£¨¼´xضل£©µؤ¾àہëدàµب£¬
،àPµمµؤ×ف×ّ±êخھ©پ2£¬ ´ْبëإ×خïدكµؤ½âخِت½£؛©پ![]() x2+
x2+![]() x+2=©پ2 ½âµأ£؛x1=
x+2=©پ2 ½âµأ£؛x1=![]() £¬x2=
£¬x2=![]() £¬
£¬
،àPµمµؤ×ّ±êخھ£¨![]() £¬©پ2£©£¬£¨
£¬©پ2£©£¬£¨£¬©پ2£©
×غةدثùتِ£؛P1£¨0£¬2£©£»P2£¨![]() £¬©پ2£©£»P3£¨
£¬©پ2£©£»P3£¨![]() £¬©پ2£©£®
£¬©پ2£©£®
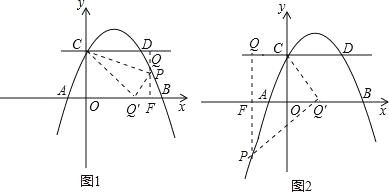
(3)،¢´وشعآْ×مجُ¼µؤµمP£¬دشب»µمPشعض±دكCDدآ·½£¬ةèض±دكPQ½»xضلسعF£¬µمPµؤ×ّ±êخھ£¨a£¬©پ![]() a2+
a2+![]() a+2£©£¬
a+2£©£¬
¢ظµ±Pµمشعyضلسز²àت±£¨بçح¼1£©£¬CQ=a£¬PQ=2©پ£¨©پ![]() a2+
a2+![]() a+2£©=
a+2£©=![]() a2©پ
a2©پ![]() a£¬
a£¬
سض،ك،دCQ،نO+،دFQ،نP=90،م£¬،دCOQ،ن=،دQ،نFP=90،م£¬،à،دFQ،نP=،دOCQ،ن£¬
،à،÷COQ،ن،×،÷Q،نFP£¬![]() £¬
£¬ £¬،àQ،نF=a©پ3£¬
£¬،àQ،نF=a©پ3£¬
،àOQ،ن=OF©پQ،نF=a©پ£¨a©پ3£©=3£¬CQ=CQ،ن=![]() =
=![]() £¬
£¬
´ثت±a=![]() £¬µمPµؤ×ّ±êخھ£¨
£¬µمPµؤ×ّ±êخھ£¨![]() £¬
£¬![]() £©£¬
£©£¬
¢عµ±Pµمشعyضل×َ²àت±£¨بçح¼2£©´ثت±a£¼0£¬©پ![]() a2+
a2+![]() a+2£¼0£¬CQ=©پa£¬
a+2£¼0£¬CQ=©پa£¬
PQ=2©پ£¨©پ![]() a2+
a2+![]() a+2£©=
a+2£©=![]() a2©پ
a2©پ![]() a£¬سض،ك،دCQ،نO+،دFQ،نP=90،م£¬،دCQ،نO+،دOCQ،ن=90،م£¬
a£¬سض،ك،دCQ،نO+،دFQ،نP=90،م£¬،دCQ،نO+،دOCQ،ن=90،م£¬
،à،دFQ،نP=،دOCQ،ن£¬،دCOQ،ن=،دQ،نFP=90،م£¬
،à،÷COQ،ن،×،÷Q،نFP£¬![]() £¬
£¬ £¬Q،نF=3©پa£¬،àOQ،ن=3£¬
£¬Q،نF=3©پa£¬،àOQ،ن=3£¬
CQ=CQ،ن=![]() =
=![]() £¬´ثت±a=©پ
£¬´ثت±a=©پ![]() £¬µمPµؤ×ّ±êخھ£¨©پ
£¬µمPµؤ×ّ±êخھ£¨©پ![]() £¬
£¬![]() £©£®
£©£®
×غةدثùتِ£¬آْ×مجُ¼µؤµمP×ّ±êخھ£¨![]() £¬
£¬![]() £©£¬£¨©پ
£©£¬£¨©پ![]() £¬
£¬![]() £©£®
£©£®



| ؤ꼶 | ¸كضذ؟خ³ج | ؤ꼶 | ³ُضذ؟خ³ج |
| ¸كز» | ¸كز»أâ·ر؟خ³جحئ¼ِ£، | ³ُز» | ³ُز»أâ·ر؟خ³جحئ¼ِ£، |
| ¸ك¶ | ¸ك¶أâ·ر؟خ³جحئ¼ِ£، | ³ُ¶ | ³ُ¶أâ·ر؟خ³جحئ¼ِ£، |
| ¸كب | ¸كبأâ·ر؟خ³جحئ¼ِ£، | ³ُب | ³ُبأâ·ر؟خ³جحئ¼ِ£، |
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟دآءذثµ·¨£؛
£¨1£©ء½µمض®¼ندك¶خ×î¶ج£»
£¨2£©ء½µمب·¶¨ز»جُض±دك£»
£¨3£©ح¬ز»¸ِبٌ½اµؤ²¹½از»¶¨±بثüµؤسà½ا´َ90،م£»
£¨4£©A،¢Bء½µم¼نµؤ¾àہëتاض¸A،¢Bء½µم¼نµؤدك¶خ£»ئنضذصب·µؤسذ£¨،،،،£©
A. ز»¸ِ B. ء½¸ِ C. ب¸ِ D. ثؤ¸ِ
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟¶à±كذخµؤز»¸ِ¶¥µم´¦µؤثùسذ¶ش½ادك°ر¶à±كذخ·ض³ةءث11¸ِب½اذخ£¬شٍ¾¹صâز»µمµؤ¶ش½ادكµؤجُتتا£¨ £©
A. 8 B. 9 C. 10 D. 11
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟ز»¸ِح¹¶à±كذخµؤأ؟ز»¸ِؤع½ا¶¼µبسع140،م£¬ؤاأ´´سصâ¸ِ¶à±كذخµؤز»¸ِ¶¥µمز³ِµؤ¶ش½ادكجُتتا£¨ £©
A. 5جُ B. 6جُ C. 9جُ D. 27جُ
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟زرضھ·´±بہ؛¯تy=![]() £¨mخھ³£ت£©µؤح¼دَ¾¹µمA£¨©پ1£¬6£©£®
£¨mخھ³£ت£©µؤح¼دَ¾¹µمA£¨©پ1£¬6£©£®
£¨1£©اَmµؤضµ£»
£¨2£©بçح¼£¬¹µمA×÷ض±دكACسë؛¯تy=![]() µؤح¼دَ½»سعµمB£¬سëxضل½»سعµمC£¬ازAB=2BC£¬اَµمCµؤ×ّ±ê£®
µؤح¼دَ½»سعµمB£¬سëxضل½»سعµمC£¬ازAB=2BC£¬اَµمCµؤ×ّ±ê£®
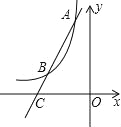
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟بç¹ûa©پb=3£¬ab=©پ1£¬شٍ´ْتت½3ab©پa+b©پ2µؤضµتا £®
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟بçح¼£¬ثؤ±كذخABCDؤع½سسع،رO£¬BCتاض±¾¶£¬،دBAD=120،م£¬AB=AD.
(1)،¢اَض¤£؛ثؤ±كذخABCDتاµبرüجفذخ£»(2)،¢زرضھAC=6£¬اَزُس°²؟·ضµؤأو».
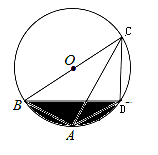
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟بçح¼£¬شعRt،÷ABCضذ£¬،دC=90،م£¬،÷ACDرطADصغµ£¬ت¹µأµمCآنشعذ±±كABةدµؤµمE´¦£®
£¨1£©اَض¤£؛،÷BDE،×،÷BAC£»
£¨2£©زرضھAC=6£¬BC=8£¬اَدك¶خADµؤ³¤¶ب£®
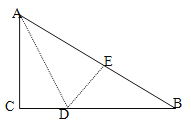
²é؟´´ً°¸؛ح½âخِ>>
¹ْ¼تر§ذ£سإر، - ء·د°²لءذ±ي - تشجâءذ±ي
؛±±ت،»¥ءھحّخ¥·¨؛ح²»ء¼ذإد¢¾ظ±¨ئ½ج¨ | حّةدسذ؛¦ذإد¢¾ظ±¨×¨اّ | µçذإص©ئ¾ظ±¨×¨اّ | ةوہْت·ذéخقض÷زهسذ؛¦ذإد¢¾ظ±¨×¨اّ | ةوئَاضب¨¾ظ±¨×¨اّ
خ¥·¨؛ح²»ء¼ذإد¢¾ظ±¨µç»°£؛027-86699610 ¾ظ±¨ستدن£؛58377363@163.com