【题目】分解因式a2-2a=______________．
互动课堂系列答案
激活思维智能训练课时导学练系列答案科目：初中数学 来源： 题型：
【题目】如图，∠1+∠2=180°，∠3=∠B，试判断∠AED与∠C的大小关系，并证明你的结论． 
解：∠C与∠AED相等，理由如下：
∵∠1+∠2=180°（已知），∠1+∠DFE=180°（邻补角定义）
∴∠2= ． （ ． ），
∴AB∥EF（ ． ）
∴∠3= ． （ ． ）
又∠B=∠3（已知）
∴∠B= ． （等量代换）
∴DE∥BC（ ． ）
∴∠C=∠AED（ ． ）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】高速公路的同一侧有A、B两城镇，如图，它们到高速公路所在直线MN的距离分别为AA′＝2 km，BB′＝4 km，A′B′＝8 km.要在高速公路上A′、B′之间建一个出口P，使A、B两城镇到P的距离之和最小．求这个最短距离．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在学习了利用尺规作一个角的平分线后，爱钻研的小聪发现，只有一把刻度尺也可以作出一个角的平分线．她是这样作的(如图)：
(1)分别在∠AOB的两边OA，OB上各取一点C，D，使得OC＝OD.
(2)连结CD，并量出CD的长度，取CD的中点E.
(3)过O，E两点作射线OE，则OE就是∠AOB的平分线．
请你说出小聪这样作的理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，抛物线y=ax2+bx+2交x轴于A（﹣1，0），B（4，0）两点，交y轴于点C，与过点C且平行于x轴的直线交于另一点D，点P是抛物线上一动点．
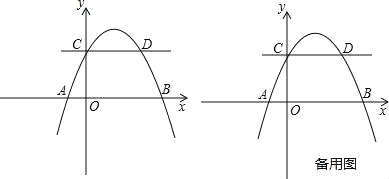
（1）求抛物线解析式及点D坐标；
（2）点E在x轴上，若以A，E，D，P为顶点的四边形是平行四边形，求此时点P的坐标；
（3）过点P作直线CD的垂线，垂足为Q，若将△CPQ沿CP翻折，点Q的对应点为Q′．是否存在点P，使Q′恰好落在x轴上？若存在，求出此时点P的坐标；若不存在，说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中，O为坐标原点．
(1)已知点A(3，1)，连接OA，平移线段OA，使点O落在点B.设点A落在点C，作如下探究：
探究一：若点B的坐标为(1，2)，请在图①中作出平移后的图形，则点C的坐标是______；连接AC、BO，请判断O、A、C、B四点构成的图形的形状，并说明理由；
探究二：若点B的坐标为(6，2)，如图②，判断O、A、B、C四点构成的图形的形状．
(2)通过上面的探究，请直接回答下列问题：
①若已知三点A（a，b）、B（c，d）、C（a+c，b+d）(点A、B、C都不与原点O重合)，顺次连接点O、A、C、B，请判断所得图形的形状；
②在①的条件下，如果所得图形是菱形或者正方形，请选择一种情况，写出a、b、c、d应满足的关系式．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，有下列判定，其中正确的有（ ） ①若∠1=∠3，则AD∥BC；
②若AD∥BC，则∠1=∠2=∠3；
③若∠1=∠3，AD∥BC，则∠1=∠2；
④若∠C+∠3+∠4=180°，则AD∥BC．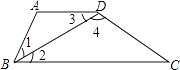
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
