
【题目】已知反比例函数y=![]() (m为常数)的图象经过点A(﹣1,6).
(m为常数)的图象经过点A(﹣1,6).
(1)求m的值;
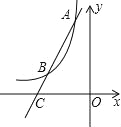
(2)如图,过点A作直线AC与函数y=![]() 的图象交于点B,与x轴交于点C,且AB=2BC,求点C的坐标.
的图象交于点B,与x轴交于点C,且AB=2BC,求点C的坐标.
【答案】(1)、m=2;(2)、(-4,0)
【解析】
试题分析:(1)、将A点坐标代入反比例函数解析式即可得到一个关于m的一元一次方程,求出m的值;(2)、分别过点A、B作x轴的垂线,垂足分别为点E、D,则△CBD∽△CAE,运用相似三角形知识求出CD的长即可求出点C的横坐标.
试题解析:(1)、∵图象过点A(﹣1,6),∴![]() =6,解得m=2.
=6,解得m=2.
(2)、分别过点A、B作x轴的垂线,垂足分别为点E、D,由题意得,AE=6,OE=1,即A(﹣1,6),
∵BD⊥x轴,AE⊥x轴,∴AE∥BD,∴△CBD∽△CAE,∴![]() =
=![]() ,∵AB=2BC,∴
,∵AB=2BC,∴![]() =
=![]() ,∴
,∴![]() =
=![]() ,
,
∴BD=2.即点B的纵坐标为2.当y=2时,x=﹣3,即B(﹣3,2),
设直线AB解析式为:y=kx+b,把A和B代入得:![]() ,解得
,解得![]() ,
,
∴直线AB解析式为y=2x+8,令y=0,解得x=﹣4,∴C(﹣4,0).



科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,A(a,0),C(b,2),且满足 ![]() ,过C作CB⊥x轴于B.
,过C作CB⊥x轴于B.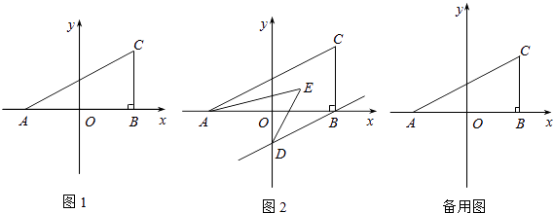
(1)求△ABC的面积.
(2)若过B作BD∥AC交y轴于D,且AE,DE分别平分∠CAB,∠ODB,如图2,求∠AED的度数.
(3)在y轴上是否存在点P,使得△ABC和△ACP的面积相等?若存在,求出P点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一枚质地均匀的骰子,骰子的六个面上分别刻有1到6的点数,投掷这样的骰子一次,向上一面点数是偶数的结果有( )
A.1种
B.2种
C.3种
D.6种
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】端午节”是我国的传统佳节,民间历来有吃“粽子”的习俗.我市某食品厂为了解市民对去年销量较好的肉馅粽、豆沙馅粽、红枣馅粽、蛋黄馅粽(以下分别用A、B、C、D表示)这四种不同口味粽子的喜爱情况,在节前对某居民区市民进行了抽样调查,并将调查情况绘制成如下两幅统计图(尚不完整).
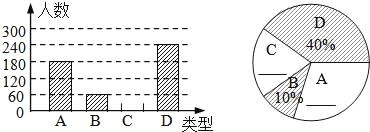
请根据以上信息回答:
(1)本次参加抽样调查的居民有多少人?
(2)将两幅不完整的图补充完整;
(3)若居民区有8000人,请估计爱吃D粽的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+2交x轴于A(﹣1,0),B(4,0)两点,交y轴于点C,与过点C且平行于x轴的直线交于另一点D,点P是抛物线上一动点.
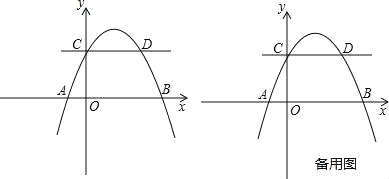
(1)求抛物线解析式及点D坐标;
(2)点E在x轴上,若以A,E,D,P为顶点的四边形是平行四边形,求此时点P的坐标;
(3)过点P作直线CD的垂线,垂足为Q,若将△CPQ沿CP翻折,点Q的对应点为Q′.是否存在点P,使Q′恰好落在x轴上?若存在,求出此时点P的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
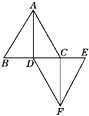
【题目】如图,已知△ABC和△DEF是两个边长都为1 cm的等边三角形,且B,D,C,E都在同一直线上,连接AD及CF.
(1)求证:四边形ADFC是平行四边形;
(2)若BD=0.3 cm,△ABC沿着BE的方向以每秒1 cm的速度运动,设△ABC的运动时间为t秒.
①当t为何值时, ![]() ADFC是菱形?请说明你的理由;
ADFC是菱形?请说明你的理由;
②![]() ADFC有可能是矩形吗?若可能,求出t的值及此矩形的面积;若不可能,请说明理由.
ADFC有可能是矩形吗?若可能,求出t的值及此矩形的面积;若不可能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com