
【题目】如图1,在平面直角坐标系中,A(a,0),C(b,2),且满足 ![]() ,过C作CB⊥x轴于B.
,过C作CB⊥x轴于B.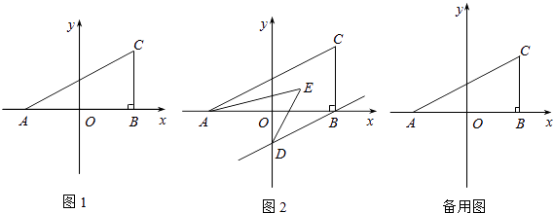
(1)求△ABC的面积.
(2)若过B作BD∥AC交y轴于D,且AE,DE分别平分∠CAB,∠ODB,如图2,求∠AED的度数.
(3)在y轴上是否存在点P,使得△ABC和△ACP的面积相等?若存在,求出P点坐标;若不存在,请说明理由.
【答案】
(1)
解:∵(a+2)2+ ![]() =0,
=0,
∴a=2=0,b﹣2=0,
∴a=﹣2,b=2,
∵CB⊥AB
∴A(﹣2,0),B(2,0),C(2,2),
∴△ABC的面积= ![]() ×2×4=4
×2×4=4
(2)
解:∵CB∥y轴,BD∥AC,
∴∠CAB=∠5,∠ODB=∠6,∠CAB+∠ODB=∠5+∠6=90°,
过E作EF∥AC,如图①,
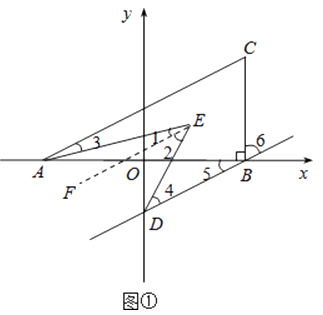
∵BD∥AC,
∴BD∥AC∥EF,
∵AE,DE分别平分∠CAB,∠ODB,
∴∠3= ![]() ∠CAB=∠1,∠4=
∠CAB=∠1,∠4= ![]() ∠ODB=∠2,
∠ODB=∠2,
∴∠AED=∠1+∠2= ![]() (∠CAB+∠ODB)=45°
(∠CAB+∠ODB)=45°
(3)
解:①当P在y轴正半轴上时,如图②,
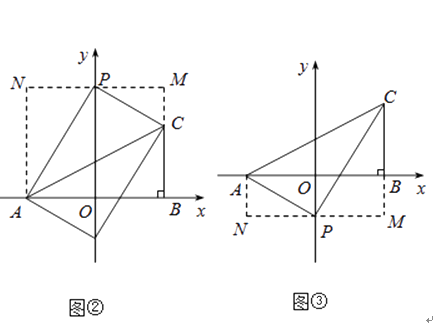
设P(0,t),
过P作MN∥x轴,AN∥y轴,BM∥y轴,
∵S△APC=S梯形MNAC﹣S△ANP﹣S△CMP=4,
∴ ![]() ﹣t﹣(t﹣2)=4,解得t=3,
﹣t﹣(t﹣2)=4,解得t=3,
②当P在y轴负半轴上时,如图③
∵S△APC=S梯形MNAC﹣S△ANP﹣S△CMP=4
∴ ![]() +t﹣(2﹣t)=4,解得t=﹣1,
+t﹣(2﹣t)=4,解得t=﹣1,
∴P(0,﹣1)或(0,3)
【解析】(1)根据非负数的性质易得a=﹣2,b=2,然后根据三角形面积公式计算;(2)过E作EF∥AC,根据平行线性质得BD∥AC∥EF,且∠3= ![]() ∠CAB=∠1,∠4=
∠CAB=∠1,∠4= ![]() ∠ODB=∠2,所以∠AED=∠1+∠2=
∠ODB=∠2,所以∠AED=∠1+∠2= ![]() (∠CAB+∠ODB);然后把∠CAB+∠ODB=∠5+∠6=90° 代入计算即可;(3)分类讨论:设P(0,t),当P在y轴正半轴上时,过P作MN∥x轴,AN∥y轴,BM∥y轴,利用S△APC=S梯形MNAC﹣S△ANP﹣S△CMP=4可得到关于t的方程,再解方程求出t;
(∠CAB+∠ODB);然后把∠CAB+∠ODB=∠5+∠6=90° 代入计算即可;(3)分类讨论:设P(0,t),当P在y轴正半轴上时,过P作MN∥x轴,AN∥y轴,BM∥y轴,利用S△APC=S梯形MNAC﹣S△ANP﹣S△CMP=4可得到关于t的方程,再解方程求出t;
当P在y轴负半轴上时,运用同样方法可计算出t.
【考点精析】掌握平行线的判定与性质和三角形的面积是解答本题的根本,需要知道由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质;三角形的面积=1/2×底×高.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知射线AB与直线CD交于点O,OF平分∠BOC,OG⊥OF于O,AE∥OF,且∠A=30°. 
(1)求∠DOF的度数;
(2)试说明OD平分∠AOG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题8分)如图1,平行四边形ABCD中,点O是对角线AC的中点,EF过点O,与AD,BC分别相交于点E,F,GH过点O,与AB,CD分别相交于点G,H,连接EG,FG,FH,EH.

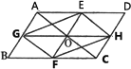
(1)求证:四边形EGFH是平行四边形;
(2)如图2,若EF//AB,GH//BC,在不添加任何辅助线的情况下,请直接写出图2中与四边形AGHD面积相等的所有平行四边形(四边形AGHD除外).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙、丁四位选手各射击10次,每人的平均成绩都是9.3环,方差如表:
选手 | 甲 | 乙 | 丙 | 丁 |
方差(环2) | 0.035 | 0.016 | 0.022 | 0.025 |
则这四个人种成绩发挥最稳定的是( )
A.甲B.乙C.丙D.丁
查看答案和解析>>
科目:初中数学 来源: 题型:
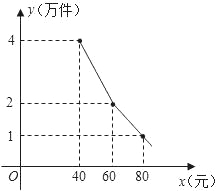
【题目】为了扶持大学生自主创业,市政府提供了80万元无息贷款,用于某大学生开办公司生产并销售自主研发的一种电子产品,并约定用该公司经营的利润逐步偿还无息贷款.已知该产品的生产成本为每件40元,员工每人每月的工资为2500元,公司每月需支付其它费用15万元.该产品每月销售量y(万件)与销售单价x(元)之间的函数关系如图所示.
(1)求月销售量y(万件)与销售单价x(元)之间的函数关系式;
(2)当销售单价定为50元时,为保证公司月利润达到5万元(利润=销售额﹣生产成本﹣员工工资﹣其它费用),该公司可安排员工多少人?
(3)若该公司有80名员工,则该公司最早可在几个月后还清无息贷款?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:
(1)两点之间线段最短;
(2)两点确定一条直线;
(3)同一个锐角的补角一定比它的余角大90°;
(4)A、B两点间的距离是指A、B两点间的线段;其中正确的有( )
A. 一个 B. 两个 C. 三个 D. 四个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF.
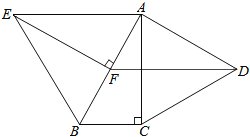
(1)试说明AC=EF;
(2)求证:四边形ADFE是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数y=![]() (m为常数)的图象经过点A(﹣1,6).
(m为常数)的图象经过点A(﹣1,6).
(1)求m的值;
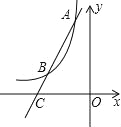
(2)如图,过点A作直线AC与函数y=![]() 的图象交于点B,与x轴交于点C,且AB=2BC,求点C的坐标.
的图象交于点B,与x轴交于点C,且AB=2BC,求点C的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com