练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】下列说法：

    （1）两点之间线段最短；

    （2）两点确定一条直线；

    （3）同一个锐角的补角一定比它的余角大90°；

    （4）A、B两点间的距离是指A、B两点间的线段；其中正确的有（　　）

    A. 一个 B. 两个 C. 三个 D. 四个

    【答案】C

    【解析】

    （1）根据线段的性质即可求解；

    （2）根据直线的性质即可求解；

    （3）余角和补角一定指的是两个角之间的关系，同角的补角比余角大90°；

    （4）根据两点间的距离的定义即可求解．

    （1）两点之间线段最短是正确的；

    （2）两点确定一条直线是正确的；

    （3）同一个锐角的补角一定比它的余角大90°是正确的；

    （4）A、B两点间的距离是指A、B两点间的线段的长度，原来的说法是错误的．

    故选C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】将数字“6”旋转180°，得到数字“9”，将数字“9”旋转180°，得到数字“6”，现将数字“69”旋转180°，得到的数字是（ ）
    A.96
    B.69
    C.66
    D.99

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】有一个一次函数的图象，甲、乙两位同学分别说出了它的一些特点：

    甲：y随x的增大而减小； 乙：当x＜0时，y＞3．

    请你写出满足甲、乙两位同学要求的一个一次函数表达式____________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

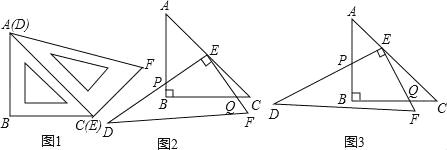
    【题目】如图1，一副直角三角板满足AB=BC，AC=DE，∠ABC=∠DEF=90°，∠EDF=30°，

    【操作1】将三角板DEF的直角顶点E放置于三角板ABC的斜边AC上，再将三角板DEF绕点E旋转，并使边DE与边AB交于点P，边EF与边BC于点Q．

    在旋转过程中，如图2，当时，EP与EQ满足怎样的数量关系？并给出证明．

    【操作2】在旋转过程中，如图3，当时EP与EQ满足怎样的数量关系？，并说明理由．

    【总结操作】根据你以上的探究结果，试写出当时，EP与EQ满足的数量关系是什么？其中m的取值范围是什么？（直接写出结论，不必证明）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，在平面直角坐标系中，A（a，0），C（b，2），且满足 ，过C作CB⊥x轴于B．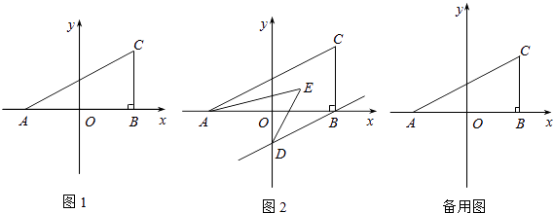

    （1）求△ABC的面积．
    （2）若过B作BD∥AC交y轴于D，且AE，DE分别平分∠CAB，∠ODB，如图2，求∠AED的度数．
    （3）在y轴上是否存在点P，使得△ABC和△ACP的面积相等？若存在，求出P点坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，∠1+∠2=180°，∠3=∠B，试判断∠AED与∠C的大小关系，并证明你的结论．
    解：∠C与∠AED相等，理由如下：
    ∵∠1+∠2=180°（已知），∠1+∠DFE=180°（邻补角定义）
    ∴∠2= ． （ ． ），
    ∴AB∥EF（ ． ）
    ∴∠3= ． （ ． ）
    又∠B=∠3（已知）
    ∴∠B= ． （等量代换）
    ∴DE∥BC（ ． ）
    ∴∠C=∠AED（ ． ）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，平面直角坐标系中，已知点A（﹣3，3），B（﹣5，1），C（﹣2，0），P（a，b）是△ABC的边AC上任意一点，△ABC经过平移后得到△A1B1C1 ， 点P的对应点为P1（a+6，b﹣2）．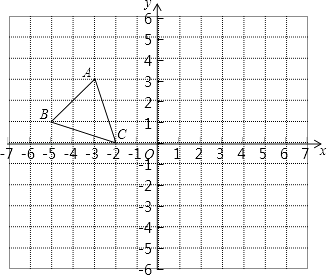

    （1）直接写出点C1的坐标；
    （2）在图中画出△A1B1C1；
    （3）求△AOA1的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】合并同类项：12x﹣20x=_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线y=ax2+bx+2交x轴于A（﹣1，0），B（4，0）两点，交y轴于点C，与过点C且平行于x轴的直线交于另一点D，点P是抛物线上一动点．

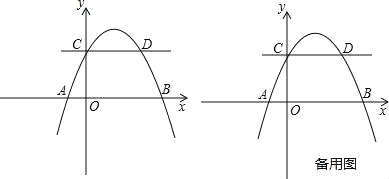
    （1）求抛物线解析式及点D坐标；

    （2）点E在x轴上，若以A，E，D，P为顶点的四边形是平行四边形，求此时点P的坐标；

    （3）过点P作直线CD的垂线，垂足为Q，若将△CPQ沿CP翻折，点Q的对应点为Q′．是否存在点P，使Q′恰好落在x轴上？若存在，求出此时点P的坐标；若不存在，说明理由．

    查看答案和解析>>

    同步练习册答案