
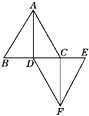
����Ŀ����ͼ����֪��ABC�͡�DEF�������߳���Ϊ1 cm�ĵȱ������Σ���B��D��C��E����ͬһֱ���ϣ�����AD��CF.
(1)��֤���ı���ADFC��ƽ���ı��Σ�
(2)��BD��0.3 cm����ABC����BE�ķ�����ÿ��1 cm���ٶ��˶������ABC���˶�ʱ��Ϊt�룮
�ٵ�tΪ��ֵʱ�� ![]() ADFC�����Σ���˵��������ɣ�
ADFC�����Σ���˵��������ɣ�
��![]() ADFC�п����Ǿ����������ܣ����t��ֵ���˾��ε�������������ܣ���˵�����ɣ�
ADFC�п����Ǿ����������ܣ����t��ֵ���˾��ε�������������ܣ���˵�����ɣ�
���𰸡�������
�������������������1��������֪������֪AC��DF�����ɵó��ı���ADFC��ƽ���ı��Σ�
��2��������ABC����BE�ķ�����ÿ��1cm���ٶ��˶������Ե�t=![]() ��ʱ��B��D�غϣ���ʱ�ı���Ϊ���Σ�
��ʱ��B��D�غϣ���ʱ�ı���Ϊ���Σ�
��3����ƽ���ı���ADFC�Ǿ��Σ����ADF=90����E��B�غϣ��ó�t=1.3�룬�������ʱ���ε������
���������
��1������ABC����DEF�������߳���Ϊlcm�ĵȱ������Σ�
��AC=DF=1cm����ACB=��FDE=60����
��AC��DF��
���ı���ADFC��ƽ���ı��Σ�
��2���ٵ�t=0.3��ʱ��ƽ���ı���ADFC�����Σ��������£�
����ABC����BE�ķ�����ÿ��1cm���ٶ��˶���
�൱t=![]() ��ʱ��B��E�غϣ���ͼ��ʾ��
��ʱ��B��E�غϣ���ͼ��ʾ��

��AD=AE=BC=DE=DF=EF��
��ƽ���ı���ADFC�����Σ�
����ƽ���ı���ADFC�Ǿ���,���ADF=90����
���ADC=9060=30��
ͬ����DAB=30��=��ADC��
��BA=BD��
ͬ��EC=EF��
��E��B�غϣ�
��t=(1+0.3)��1=1.3�룬
��ʱ����ͼ��
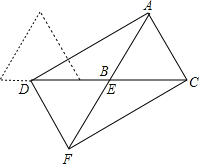
��Rt��ADF��
��ADF=90����DF=1cm��AF=2cm��
��AD=![]() cm��
cm��
�����ADFC�����=AD��DF=![]() cm2.
cm2.


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ֱ���Rt��ABC��ֱ�DZ�AC��б��AB�������ȱ���ACD���ȱ���ABE����֪��BAC=30����EF��AB������ΪF������DF��
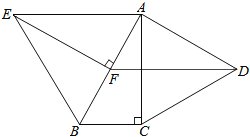
��1����˵��AC=EF��
��2����֤���ı���ADFE��ƽ���ı��Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ����һ�ࡢ�����90��ѧ���������һ��ת��4��ͬѧ�����࣬��ôһ���ѧ�������Ƕ����80%��������ԭ�����ж�����ѧ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
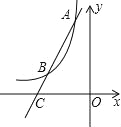
����Ŀ����֪����������y=![]() ��mΪ��������ͼ����A����1��6����
��mΪ��������ͼ����A����1��6����
��1����m��ֵ��
��2����ͼ������A��ֱ��AC�뺯��y=![]() ��ͼ���ڵ�B����x�ύ�ڵ�C����AB=2BC�����C�����꣮
��ͼ���ڵ�B����x�ύ�ڵ�C����AB=2BC�����C�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������x��һԪ���η���x2+kx��2��0��kΪʵ������������ǣ�������
A.����������ȵ�ʵ����B.��������ȵ�ʵ����
C.û��ʵ����D.����ȷ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������a��b�Ķ���ʽ3��a2��2ab��b2������a2+mab+2b2���в�����ab���m= ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪���ı���ABCD�У�AD��BC��AC��BD����E��F��G��H��P��Q�ֱ���AB��BC��CD��DA��AC��BD���е㣮
��֤��(1)�ı���EFGH�Ǿ��Σ�
(2)�ı���EQGP�����Σ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����m2-n2=6����m-n=3����m+n =_______________
���𰸡�2
����������������m2-n2=��m+n����m-n��=3��m+n��=6��
��m+n=2.
�����͡������
��������
13
����Ŀ�����4x2+ax+9��һ����ȫƽ��ʽ����ôa��ֵΪ______.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com