
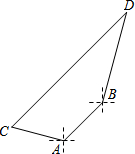
 在海岸A处,发现北偏东45°方向、距离A处20海里的B处有一艘走私船;在A处北偏西75°方向、距离A处20海里的C处的缉私船奉命以10$\sqrt{3}$海里/小时的速度追截走私船.同时,走私船正以10海里/小时的速度从B处向北偏东15°方向逃窜,问缉私船沿什么方向能最快追上走私船?最少要花多少时间?
在海岸A处,发现北偏东45°方向、距离A处20海里的B处有一艘走私船;在A处北偏西75°方向、距离A处20海里的C处的缉私船奉命以10$\sqrt{3}$海里/小时的速度追截走私船.同时,走私船正以10海里/小时的速度从B处向北偏东15°方向逃窜,问缉私船沿什么方向能最快追上走私船?最少要花多少时间? 分析 延长CA,DB交于点M,根据已知条件得:∠BAM=60°,∠ABM=30°,于是得到△CDM是直角三角形,设缉私船最少要花t小时追上走私船,根据勾股定理列方程即可求得答案.
解答 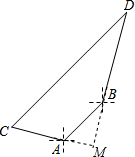 解:延长CA,DB交于点M,
解:延长CA,DB交于点M,
根据已知条件得:∠BAM=60°,∠ABM=30°,
∴∠M=90°,
∵AB=20,
∴AM=10,BM=10$\sqrt{3}$,
设缉私船最少要花t小时追上走私船,
∴CD=10$\sqrt{3}$t,CM=20+10=30,DM=10t+10$\sqrt{3}$,
∵CD2=CM2+DM2,
∴(10$\sqrt{3}$t)2=302+(10t+10$\sqrt{3}$)2,
解得:t=2$\sqrt{3}$,
∴CD=60,CM=30,
∴∠D=30,∠C=60°,
∴缉私船沿北偏东45°的方向能最快追上走私船,最少要花2$\sqrt{3}$小时.
点评 此题考查了解直角三角形的应用-方向角问题,结合航海中的实际问题,将解直角三角形的相关知识有机结合,体现了数学应用于实际生活的思想.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
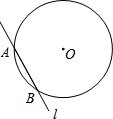 如图,⊙O的半径为1,A为⊙O上一点,过点A的直线l交⊙O于点B,将直线l绕点A旋转180°,当AB的长度由1变为$\sqrt{3}$时,l在圆内扫过的面积为( )
如图,⊙O的半径为1,A为⊙O上一点,过点A的直线l交⊙O于点B,将直线l绕点A旋转180°,当AB的长度由1变为$\sqrt{3}$时,l在圆内扫过的面积为( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{3}$或$\frac{π}{2}$+$\sqrt{3}$ | D. | $\frac{π}{6}$或$\frac{π}{2}$+$\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com