
分析 先作差得到a-b=($\sqrt{n+3}$+$\sqrt{n}$)-($\sqrt{n+1}$+$\sqrt{n+2}$),被减数和减数平方,比较它们平方的大小即可求解.
解答 解:∵a=$\sqrt{n+3}$-$\sqrt{n+1}$>0,b=$\sqrt{n+2}$-$\sqrt{n}$>0,
a-b=($\sqrt{n+3}$+$\sqrt{n}$)-($\sqrt{n+1}$+$\sqrt{n+2}$),
($\sqrt{n+3}$+$\sqrt{n}$)2=n+3+2$\sqrt{n(n+3)}$+n=2n+3+2$\sqrt{n(n+3)}$,
($\sqrt{n+1}$+$\sqrt{n+2}$)2=n+1+2$\sqrt{{n}^{2}+3n+2}$+n+2=2n+3+2$\sqrt{{n}^{2}+3n+2}$,
2n+3+2$\sqrt{n(n+3)}$<2n+3+2$\sqrt{{n}^{2}+3n+2}$,
∴a-b<0,
∴a<b.
点评 此题考查了实数大小比较,关键是熟悉作差法比较大小的方法.


科目:初中数学 来源: 题型:解答题
 正方形ABCD中,点P为边AD上的一点,DE⊥CP于E,延长CP到F,使得CE=EF,连接DF、AF,过点D作∠ADF的角平分线,交CF于H,连结BH.
正方形ABCD中,点P为边AD上的一点,DE⊥CP于E,延长CP到F,使得CE=EF,连接DF、AF,过点D作∠ADF的角平分线,交CF于H,连结BH.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
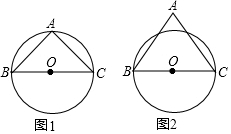 已知BC是⊙O的直径,△ABC为等腰三角形,请仅用无刻度的直尺完成下列作图.
已知BC是⊙O的直径,△ABC为等腰三角形,请仅用无刻度的直尺完成下列作图.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
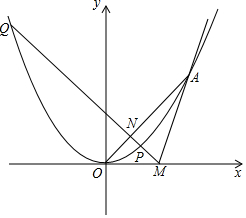 已知抛物线y=ax2(a>0),直线l:y=kx-2k,直线l与x轴交于点M,与抛物线交于唯一的公共点A(异于点O),且满足:MA=2$\sqrt{5}$,直线MQ与抛物线交于P、Q两点,与直线OA交于点N
已知抛物线y=ax2(a>0),直线l:y=kx-2k,直线l与x轴交于点M,与抛物线交于唯一的公共点A(异于点O),且满足:MA=2$\sqrt{5}$,直线MQ与抛物线交于P、Q两点,与直线OA交于点N查看答案和解析>>
科目:初中数学 来源: 题型:解答题
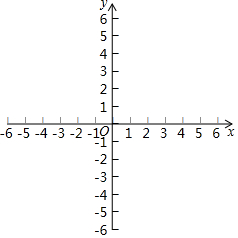 如图,在平面直角坐标系中,二次函数y=ax2+bx+c的图象经过点A(-2,0),B(0,-2$\sqrt{3}$),C(4,0),其中对称轴与x轴交于点D.
如图,在平面直角坐标系中,二次函数y=ax2+bx+c的图象经过点A(-2,0),B(0,-2$\sqrt{3}$),C(4,0),其中对称轴与x轴交于点D.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 必有1次标有2个点数的面朝上 | B. | 必有2次标有3个点数的面朝上 | ||
| C. | 可能有1次标有4个点数的面朝上 | D. | 不可能有1次标有1个点数的面朝上 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com