
 已知:E是正方形ABCD内一点,且∠ECD=∠EDC=15°,求证:△ABE是等边三角形,小萍同学灵活运用全等变换,将△ECD进行旋转与翻折,使△ECD≌△FAD,巧妙地解答了此题.请按照小萍的思路,探究并解答下列问题:
已知:E是正方形ABCD内一点,且∠ECD=∠EDC=15°,求证:△ABE是等边三角形,小萍同学灵活运用全等变换,将△ECD进行旋转与翻折,使△ECD≌△FAD,巧妙地解答了此题.请按照小萍的思路,探究并解答下列问题: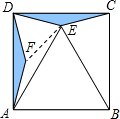
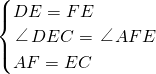 ,
,

 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:初中数学 来源: 题型:
 如图,已知点P是线段AB的黄金分割点,且PA>PB,若S1表示以PA为边的正方形的面积,S2表示长为AB、宽为PB的矩形的面积,那么S1( )S2.
如图,已知点P是线段AB的黄金分割点,且PA>PB,若S1表示以PA为边的正方形的面积,S2表示长为AB、宽为PB的矩形的面积,那么S1( )S2.| A、> | B、= | C、< | D、无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在平面直角坐标系中,直y=
如图,在平面直角坐标系中,直y=| 3 |
| 2 |
| 16 |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
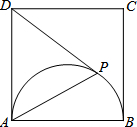 (2013•厦门质检)如图,已知四边形ABCD是正方形,以AB为直径在正方形内作半圆,P是半圆上的动点(不与点A、B重合),连接PA、PD.
(2013•厦门质检)如图,已知四边形ABCD是正方形,以AB为直径在正方形内作半圆,P是半圆上的动点(不与点A、B重合),连接PA、PD.查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com