
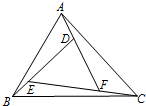
 如图,D、E、F是△ABC内的三个点,且D在AF上,F在CE上,E在BD上.若CF=$\frac{1}{2}$EF,AD=$\frac{1}{3}$FD,BE=$\frac{1}{4}$DE,△DEF的面积是1,则△ABC的面积是$\frac{59}{24}$.
如图,D、E、F是△ABC内的三个点,且D在AF上,F在CE上,E在BD上.若CF=$\frac{1}{2}$EF,AD=$\frac{1}{3}$FD,BE=$\frac{1}{4}$DE,△DEF的面积是1,则△ABC的面积是$\frac{59}{24}$. 分析 分别连接AE、DC、FB,利用三角形的面积公式得到图中是6个小三角形的面积,然后将其相加.
解答 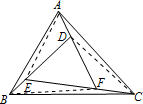 解:分别连接AE、DC、FB,
解:分别连接AE、DC、FB,
∵CF=$\frac{1}{2}$EF,
∴S△DEF=2S△DFC=1,
∴S△DFC=$\frac{1}{2}$ ①.
∵AD=$\frac{1}{3}$FD,
∴S△ADC=$\frac{1}{3}$S△DFC=$\frac{1}{6}$ ②,
S△DEF=3S△ADE=1,
∴S△ADE=$\frac{1}{3}$ ③,
∵BE=$\frac{1}{4}$DE,
∴S△ABE=$\frac{1}{4}$S△ADE=$\frac{1}{12}$ ④.
S△BEF=$\frac{1}{4}$S△DEF=$\frac{1}{4}$,⑤
∴S△BFC=$\frac{1}{2}$S△BEF=$\frac{1}{8}$ ⑥,
由①+②+③+④+⑤+⑥+1=$\frac{59}{24}$.
故答案是:$\frac{59}{24}$.
点评 此题主要考查学生对三角形面积的理解和掌握,解答此题的关键是分别连接AE、DC、FB,求出各三角形的面积.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (a+b)(a-b)=a2-b2 | B. | a2+2ab+b2=(a+b)2 | C. | a(a+b)=a2+ab | D. | (a-b)2=(b-a)2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
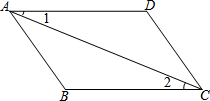 如图,已知∠1=∠2,∠B=∠D,试说明:AB∥CD
如图,已知∠1=∠2,∠B=∠D,试说明:AB∥CD查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
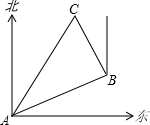 如图,在一次夏令营活动中,小明从营地A到C地去,先沿北偏东70°方向到达B地,再沿北偏西20°方向到达C地,此时∠ACB=60°,问小明在营地A的( )
如图,在一次夏令营活动中,小明从营地A到C地去,先沿北偏东70°方向到达B地,再沿北偏西20°方向到达C地,此时∠ACB=60°,问小明在营地A的( )| A. | 北偏东20°方向上 | B. | 北偏东30°方向上 | C. | 北偏西30°方向上 | D. | 北偏东40°方向上 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
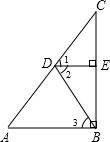 如图,∠1=∠2,DE⊥BC,AB⊥BC,那么∠A=∠3吗?说明理由.(请为每一步推理注明依据)
如图,∠1=∠2,DE⊥BC,AB⊥BC,那么∠A=∠3吗?说明理由.(请为每一步推理注明依据) 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com