
分析 方程组三个方程相加求出x+y+z的值,将每一个方程代入求出x,y,z的值即可.
解答 解:$\left\{\begin{array}{l}{x+y=3①}\\{y+z=5②}\\{z+x=4③}\end{array}\right.$,
①+②+③得:2(x+y+z)=12,即x+y+z=6④,
把①代入④得:z=3,
把②代入④得:x=1,
把③代入④得:y=2,
则方程组的解为$\left\{\begin{array}{l}{x=1}\\{y=2}\\{z=3}\end{array}\right.$.
故答案为:$\left\{\begin{array}{l}{x=1}\\{y=2}\\{z=3}\end{array}\right.$
点评 此题考查了解三元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.


科目:初中数学 来源: 题型:解答题
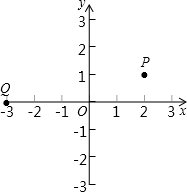 如图,已知Q点的坐标为(-3,0),将点Q向上平移一个单位长度,再向右平移5个单位长度,得到点P.
如图,已知Q点的坐标为(-3,0),将点Q向上平移一个单位长度,再向右平移5个单位长度,得到点P.查看答案和解析>>
科目:初中数学 来源:2017届福建省仙游县郊尾、枫亭五校教研小片区九年级下学期第一次月考数学试卷(解析版) 题型:填空题
若关于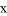 的一元二次方程
的一元二次方程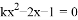 有两个不相等的实数根,则
有两个不相等的实数根,则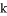 的取值范围是__________.
的取值范围是__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com