
【题目】已知直线![]() 与⊙O,AB是⊙O的直径,AD⊥
与⊙O,AB是⊙O的直径,AD⊥![]() 于点D.
于点D.
(1)如图①,当直线![]() 与⊙O相切于点C时,若∠DAC=30°,求∠BAC的大小;
与⊙O相切于点C时,若∠DAC=30°,求∠BAC的大小;
(2)如图②,当直线![]() 与⊙O相交于点E、F时,若∠DAE=18°,求∠BAF的大小.
与⊙O相交于点E、F时,若∠DAE=18°,求∠BAF的大小.

【答案】(1)30°;(2)18°.
【解析】试题分析:(1)连接OD,易证OC∥AD,所以∠OCA=∠DAC,由因为OA=OC,所以∠OAC=∠OCA;
(2)连接BE,AB是⊙O的直径,所以∠AEB=90°,从而可知∠BEF=∠DAE=18°,由圆周角定理可知:∠BAF=∠BEF=18°
试题解析:(1)连接OC、

∵l是⊙O的切线,
∴OC⊥l,
∵AD⊥l,
∴OC∥AD,
∴∠OCA=∠DAC=30°,
∵OA=OC,
∴∠OAC=∠OCA=30°,
(2)连接BE,
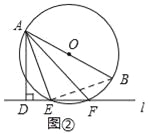
∵AB是⊙O的直径,
∴∠AEB=90°,
∴∠AED+∠BEF=90°,
∵∠AED+∠DAE=90°,
∴∠BEF=∠DAE=18°,
∵![]() ,
,
∴∠BAF=∠BEF=18°


 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案科目:初中数学 来源: 题型:
【题目】小明从家出发,沿一条直道跑步,经过一段时间原路返回,刚好在第![]() 回到家中.设小明出发第
回到家中.设小明出发第![]() 时的速度为
时的速度为![]() ,离家的距离为
,离家的距离为![]() .
.![]() 与
与![]() 之间的函数关系如图所示(图中的空心圈表示不包含这一点).
之间的函数关系如图所示(图中的空心圈表示不包含这一点).

(1)小明出发第![]() 时离家的距离为
时离家的距离为 ![]() ;
;
(2)当![]() 时,求
时,求![]() 与
与![]() 之间的函数表达式;
之间的函数表达式;
(3)画出![]() 与
与![]() 之间的函数图像.
之间的函数图像.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为创建生态文明建设城市,对公路旁的绿化带进行全面改造.现有甲、乙两个工程队,甲队单独完成这项工程,刚好如期完成,每施工一天,需付工程款1.5万元;乙工程队单独完成这项工程要比规定工期多用a天,乙工程队每施工一天需付工程款1万元.若先由甲、乙两队一起合作b天,剩下的工程由乙队单独做,也正好如期完工
(1)当a=6,b=4时,求工程预定工期的天数.
(2)若a﹣b=2.a是偶数
①求甲队、乙队单独完成工期的天数(用含a的代数式表示)
②工程领导小组有三种施工方案:
方案一:甲队单独完成这项工程;
方案二:乙队单独完成这项工程;
方案三:先由甲、乙两队一起合作b天,剩下的工程由乙队单独做.
为了节省工程款,同时又能如期完工,请你选择一种方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B与∠C的角平分线相交于点I,过点I作BC的平行线,分别交AB、AC于点D、E.若AB=9,AC=6,BC=8,则△ADE的周长是( )
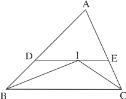
A. 14B. 15C. 17D. 23
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AD是△ABC的中线.

(1)利用尺规按下列要求作图,并在图中标明相应字母.(保留作图痕迹,不写作法)
①作线段AC的垂直平分线,分别交AC、AD、AB于点E、M、F;②连接CM、BM;
(2)若∠CAD=20°,求∠MCD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,以点
中,以点![]() 为圆心,
为圆心,![]() 长为半径画弧交
长为半径画弧交![]() 于点
于点![]() ,再分别以点
,再分别以点![]() 、
、![]() 为圆心,大于
为圆心,大于![]() 的相同长为半径画弧,两弧交于点
的相同长为半径画弧,两弧交于点![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,连接
,连接![]() ,则所得四边形
,则所得四边形![]() 是菱形.
是菱形.

(1)根据以上尺规作图的过程,求证:四边形![]() 是菱形.
是菱形.
(2)若菱形![]() 的周长为16,
的周长为16,![]() ,求菱形
,求菱形![]() 的面积及
的面积及![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:
①4ac<b2;②方程ax2+bx+c=0的两个根是x1=﹣1,x2=3;
③3a+c>0;④当y>0时,x的取值范围是﹣1≤x<3;
⑤当x<0时,y随x增大而增大.
其中结论正确的个数是( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了编撰祖国的优秀传统文化,某校组织了一次“诗词大会”,小明和小丽同时参加,其中,有一道必答题是:从如图所示的九宫格中选取七个字组成一句唐诗,其答案为“山重水复疑无路”.
(1)小明回答该问题时,对第二个字是选“重”还是选“穷”难以抉择,若随机选择其中一个,则小明回答正确的概率是 ;
(2)小丽回答该问题时,对第二个字是选“重”还是选“穷”、第四个字是选“富”还是选“复”都难以抉择,若分别随机选择,请用列表或画树状图的方法求小丽回答正确的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,对角线AC、BD相交于点O,过点C作CE∥BD,过点D作DE∥AC,CE与DE相交于点E.
(1)求证:四边形CODE是矩形.
(2)若AB=5,AC=6,求四边形CODE的周长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com