
【题目】如图,在平面直角坐标系中,直线11:y=k1x+3分别与x轴,y轴交于A(﹣3,0),B两点,与直线l2:y=k2x交于点C,S△AOC=9.
(1)求tan∠BAO的值;
(2)求出直线l2的解析式;
(3)P为线段AC上一点(不含端点),连接OP,一动点H从点O出发,沿线段OP以每秒1个单位长度的速度运动到P,再沿线段PC以每秒![]() 个单位长度的速度运动到点C后停止,请直接写出点H在整个运动过程的最少用时.
个单位长度的速度运动到点C后停止,请直接写出点H在整个运动过程的最少用时.
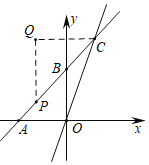
【答案】(1)1;(2)y=2x;(3)6秒.
【解析】
(1)先求直线l1的解析式,从而可以求点B,点A的坐标,求出OA和OB即可求得tan∠BAO=![]() ;
;
(2)由S△AOC=9,OA=3即可求点C的纵坐标,点C是直线l1与直线l2的交点,即可求出直线l2的解析式;
(3)过点C作CJ⊥y轴于J,过点P作PQ⊥CJ于点Q,由题意得,点H在整个运动过程的用时t=![]() =OP+QP,即点H在整个运动过程所用的时间是线段PO与PH的长度之和,也就是点O、P、Q共线时有最小值.
=OP+QP,即点H在整个运动过程所用的时间是线段PO与PH的长度之和,也就是点O、P、Q共线时有最小值.
(1)∵直线11:y=k1x+3经过点A(﹣3,0),
∴0=﹣3k1+3,即k1=1且OA=3
故直线11的解析式为:y=x+3
∴直线l1:y=x+3与y轴交点是B(0,3)即OB=3
故tan∠BAO=![]() .
.
(2)∵S△AOC=9,OA=3
∴点C到OA也就是到x轴的距离是6,由图可设C(x,6)
∵C(x,6)是直线l1:y=x+3与直线l2:y=k2x的交点
∴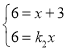 ,解得
,解得
故直线l2的解析式是:y=2x.
(3)如图,过点C作CJ⊥y轴于J,过点P作PQ⊥CJ于点Q,
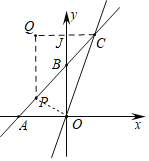
∵动点H从点O出发,沿线段OP以每秒1个单位长度的速度运动到P,遭到沿线段PC以每秒![]() 个单位长度的速度运动到点C后停止
个单位长度的速度运动到点C后停止
∴点H在整个运动过程的用时![]() ,
,
∵tan∠BAO=![]() 知∠BAO=45°
知∠BAO=45°
故∠CPQ=∠ABO=45°
∴PQ=PCcos∠CPQ=![]() =
=![]()
∴![]() 即点H在整个运动过程所用的时间是线段PO与PH的长度之和
即点H在整个运动过程所用的时间是线段PO与PH的长度之和
∴当点P与点B重合,也就是点O、P、Q共线时,OP+QP取得最小值,且(OP+QP)最小=OJ=6,
即点H在整个运动过程所用时间的最小值为6秒.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:
【题目】如图直角坐标系中,以M(3,0)为圆心的⊙M交x轴负半轴于A,交x轴正半轴于B,交y轴于C、D.
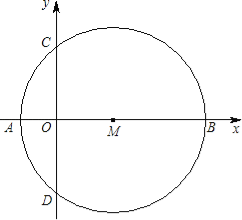
(1)若C点坐标为(0,4),求点A坐标.
(2)在(1)的条件下,在⊙M上,是否存在点P,使∠CPM=45°,若存在,求出满足条件的点P.
(3)过C作⊙M的切线CE,过A作AN⊥CE于F,交⊙M于N,当⊙M的半径大小发生变化时.AN的长度是否变化?若变化,求变化范围,若不变,证明并求值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,∠ACB=90°,∠BAC=60°,AC=6,AD平分∠BAC,交边BC于点D,过点D作CA的平行线,交边AB于点E.
中,∠ACB=90°,∠BAC=60°,AC=6,AD平分∠BAC,交边BC于点D,过点D作CA的平行线,交边AB于点E.

(1)求线段DE的长;
(2)取线段AD的中点M,联结BM,交线段DE于点F,延长线段BM交边AC于点G,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网店正在热销一款电子产品,其成本为10元/件,销售中发现,该商品每天的销售量y(件)与销售单价x(元/件)之间存在如图所示的关系:
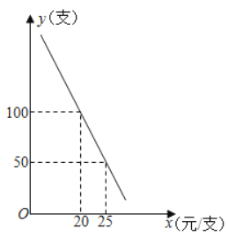
(1)请求出y与x之间的函数关系式;
(2)该款电子产品的销售单价为多少元时,每天销售利润最大?最大利润是多少元;
(3)由于武汉爆发了“新型冠状病毒”疫情,该网店店主决定从每天获得的利润中抽出300元捐赠给武汉,为了保证捐款后每天剩余利润不低于450元,如何确定该款电子产品的销售单价?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知点A,对点A作如下变换:
第一步:作点A关于x轴的对称点A1;第二步:以O为位似中心,作线段OA1的位似图形OA2,且相似比![]() =q,则称A2是点A的对称位似点.
=q,则称A2是点A的对称位似点.
(1)若A(2,3),q=2,直接写出点A的对称位似点的坐标;
(2)已知直线l:y=kx-2,抛物线C:y=-![]() x2+mx-2(m>0).点N(
x2+mx-2(m>0).点N(![]() ,2k-2)在直线l上.
,2k-2)在直线l上.
①当k=![]() 时,判断E(1,-1)是否是点N的对称位似点,请说明理由;
时,判断E(1,-1)是否是点N的对称位似点,请说明理由;
②若直线l与抛物线C交于点M(x1,y1)(x1≠0),且点M不是抛物线的顶点,则点M的对称位似点是否可能仍在抛物线C上?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣![]() x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).
x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).
(1)求抛物线的表达式;
(2)在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由;
(3)点E时线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDBF的面积最大?求出四边形CDBF的最大面积及此时E点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在面积都相等的所有矩形中,当其中一个矩形的一边长为1时,它的另一边长为3.
(1)设矩形的相邻两边长分别为x,y.
①求y关于x的函数表达式;
②当y≥3时,求x的取值范围;
(2)圆圆说其中有一个矩形的周长为6,方方说有一个矩形的周长为10,你认为圆圆和方方的说法对吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了创建全国卫生城市,某社区要清理一个卫生死角内的垃圾,租用甲、乙两车运送,两车各运12趟可完成,需支付运费4800元.已知甲、乙两车单独运完此堆垃圾,乙车所运趟数是甲车的2倍,且乙车每趟运费比甲车少200元.
(1)求甲、乙两车单独运完此堆垃圾各需运多少趟?
(2)若单独租用一台车,租用哪台车合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图①表示的是某商场2012年前四个月中两个月的商品销售额的情况,图②表示的是商场家电部各月销售额占商场当月销售总额的百分比情况,观察图①、图②解答下列问题:
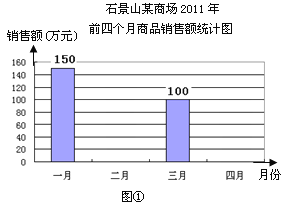
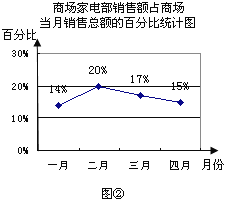
(1)商场前四个月财务结算显示四月份商场的商品销售额比一月份下降了20%,请你求出商场四月份的销售额;
(2)若商场前四个月的商品销售总额一共是500万元,请你根据这一信息将图①中的统计图补充完整;
(3)小明观察图②后认为,商场家电部四月份的销售额比三月份减少了,你同意他的看法吗?请你说明理由
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com