练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    17．小明将父亲经营的便利店中“收入100元”记作“+100元”，那么“-80元”表示（　　）
    A．支出20元B．支出80元C．收入20元D．收入80元

    分析 根据正数和负数表示相反意义的量，可得答案．

    解答 解：“收入100元”记作“+100元”，那么“-80元”表示支出80元，
    故选：B．

    点评 本题考查了正数和负数，确定相反意义的两是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    7．如图，在△ABC中，P为AB上的一点，在下列条件中：①∠ACP=∠B；②∠APC=∠ACB；③AC2=AP•AB；④AC是AP和PB的比例中项，其中能满足△APC∽△ACB的条件是（　　）
    A．①②④B．①③④C．②③④D．①②③

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．某股票市场，买、卖股票都要分别交纳印花税等有关税费．以沪市A股的股票交易为例，除成本外还要交纳：
    ①印花税：按成交金额的0.1%计算；
    ②过户费：按成交金额的0.2%计算；
    ③佣金：按不高于成交金额的0.3%计算（本题按0.3%计算），不足5元按5元计算，若某投资者以每股5.00元的价格在沪市A股中买入股票“金杯汽车”1000股，以每股5.50元的价格全部卖出，实际盈利可按如下办法求出．
    直接成本：5×1000=5000（元）；
    印花税：（5000+5.50×1000）×0.1%=10.50（元）；
    过户费：（5000+5.50×1000）×0.2%=21（元）；
    佣金：（5000+5.50×1000）×0.3%=31.50（元）
    ∵31.50＞5，∴佣金为31.50元．
    总支出：5000+10.50+21+31.50=5063（元）
    总收入：5.50×1000=5500（元）
    所以这次交易共盈利：5500-5063=437（元）
    问题：
    （1）小张以每股a（a≥5）元的价格买入以上股票1000股，当每股价格为b（b≥a）元时全部卖出，在此次交易中，小张共盈利多少元？（用含a、b的代数式表示）
    （2）小张再以每股5.00元的价格买入以上股票1000股，准备盈利1000元时才卖出，请你帮他计算卖出的价格每股是多少元？（精确到0.01元）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    5．如图，△ABC≌△EFD，且 AB=EF，EC=4，CD=3，则 AC=（　　）
    A．3B．4C．7D．8

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．OA、OB、OC是从同一端点O引出的三条不同射线，已知∠AOB=60°，∠BOC=20°，请你画出图形，并求出∠AOC的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

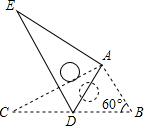    2．如图，将Rt△ABC绕点A按顺时针方向旋转一定角度得到Rt△ADE，点B的对应点D恰好落在BC边上，若DE=2，∠B=60°，则CD的长为（　　）
    A．0.5B．1.5C．$\sqrt{2}$D．1

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．如图1，抛物线y=ax2+bx-4a经过A（-1，0）、C（0，4）两点，与x轴交于另一点B．
    （1）求抛物线的解析式；
    （2）已知点D（m，m+1）在第一象限的抛物线上，求点D关于直线BC对称的点的坐标；
    （3）如图3，若抛物线的对称轴EF（E为抛物线顶点）与直线BC相交于点F，M为直线BC上的任意一点，过点M作MN∥EF交抛物线于点N，以E，F，M，N为顶点的四边形能否为平行四边形？若能，求点N的坐标；若不能，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    6．下列二次函数的图象中经过原点的是（　　）
    A．y=x2+1B．y=2x2+5xC．y=（x-2）2D．y=x2+2x-3

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    7．下列计算正确的是（　　）
    A．$\sqrt{9\frac{1}{25}}=3\frac{1}{5}$B．$\sqrt{a•b}=\sqrt{a}•\sqrt{b}$C．$（3+\sqrt{6}）÷\sqrt{3}=\sqrt{3}+2$D．$\root{3}{-8}=-2$

    查看答案和解析>>

    同步练习册答案