
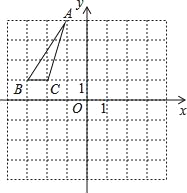
【题目】在如图所示的平面直角坐标系中,△ABC的三个顶点都在小正方形的顶点处,请结合图完成下列各题:
(1)写出tan∠ABC;AB的值;(结果保留根号).
(2)将△ABC绕原点O旋转180°,画出旋转对应的△A′B′C′,并求直线A′C′的函数表达式.
【答案】(1)tan∠ABC=![]() ;AB=
;AB=![]() ;(2)直线A′C′的函数表达式为y=3x﹣7.
;(2)直线A′C′的函数表达式为y=3x﹣7.
【解析】
(1)把∠ABC放到格点直角三角形中,利用正切的定义求它的正切值,然后利用勾股定理计算AB的长;(2)利用关于原点对称的点的坐标特征写出A′、B′、C′点的坐标,然后描点即可得到△A′B′C′,再利用待定系数法求直线A′C′的函数表达式.
(1)tan∠ABC=![]() ;AB=
;AB=![]() ;
;
(2)如图,A′(1,﹣4),B′(3,﹣1),C′(2,﹣1),△A′B′C′为所作;
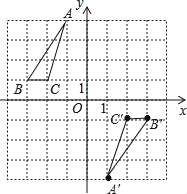
设直线A′C′的函数表达式为y=kx+b,
把A′(1,﹣4),C′(2,﹣1)代入得![]() ,解得
,解得![]() ,
,
所以直线A′C′的函数表达式为y=3x﹣7.


科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,AC为对角线,点E为AC上一点,连接EB,ED.
(1)求证:△BEC≌△DEC;
(2)延长BE交AD于点F,当∠BED=120°时,求∠EFD的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个各位数字都不为0的三位正整数N,现从它的百位、十位、个位上的数字中任意选择两个数字组成两位数若所有这些两位数的和等于这个三位数本身,则称这个三位数为本原数”例如:132,选择百位数字1和十位数字3所组成的两位数为:13和31;选择百位数字1和个位数字2所组成的两位数为:12和21;选择十位数字3和个位数字2所组成的两位数为:32和23,因为13+31+12+21+32+23=132,所以132是“本原数”
(1)判断123是不是“本原数”?请说明理由;
(2)一个三位正整数,若它的十位数字等于百位数字与个位数学的和,则称这样的三位数为“和中数”.若一个各位数字都不为0的“和中数”![]() 是“本原数”,求z与x的函数关系.
是“本原数”,求z与x的函数关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
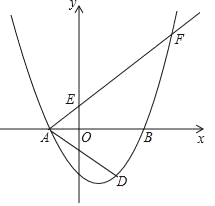
【题目】如图,在平面直角坐标系xOy中,已知抛物线y= ![]() 与x轴交于点A(﹣2,0)和点B,与y轴交于点C(0,﹣3),经过点A的射线AM与y轴相交于点E,与抛物线的另一个交点为F,且
与x轴交于点A(﹣2,0)和点B,与y轴交于点C(0,﹣3),经过点A的射线AM与y轴相交于点E,与抛物线的另一个交点为F,且![]() .
.
(1)求这条抛物线的表达式,并写出它的对称轴;
(2)求∠FAB的余切值;
(3)点D是点C关于抛物线对称轴的对称点,点P是y轴上一点,且∠AFP=∠DAB,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一天,小华和小夏玩掷骰子游戏,他们约定:他们用同一枚质地均匀的骰子各掷一次, 如果两次掷的骰子的点数相同则小华获胜:如果两次掷的骰子的点数的和是6则小夏获胜.
(1)请您列表或画树状图列举出所有可能出现的结果;
(2)请你判断这个游戏对他们是否公平并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C都在抛物线y=ax2﹣2amx+am2+2m﹣5(其中﹣![]() <a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
<a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
(1)填空:抛物线的顶点坐标为 (用含m的代数式表示);
(2)求△ABC的面积(用含a的代数式表示);
(3)若△ABC的面积为2,当2m﹣5≤x≤2m﹣2时,y的最大值为2,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
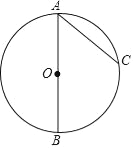
【题目】如图,AB是⊙O的直径,C是⊙O上一点,连接AC.过点B作⊙O的切线,交AC的延长线于点D,在AD上取一点E,使AE=AB,连接BE,交⊙O于点F.
请补全图形并解决下面的问题:
(1)求证:∠BAE=2∠EBD;
(2)如果AB=5,sin∠EBD=![]() .求BD的长.
.求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=k1x+b的图象与反比例函数y2=![]() 的图象相交于A,B两点,与x轴交于点C,与y轴交于点D,点B的坐标是(m,-4),连接AO,AO=5,sin∠AOC=
的图象相交于A,B两点,与x轴交于点C,与y轴交于点D,点B的坐标是(m,-4),连接AO,AO=5,sin∠AOC=![]() .
.
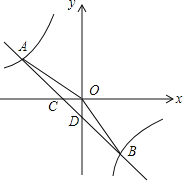
(1)求反比例函数的解析式;
(2)连接OB,求△AOB的面积;
(3)请直接写出当x<m时,y2的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,某住宅社区在相邻两楼之间修建一个上方是一个半圆,下方是长方形的仿古通道.

(1)现有一辆卡车装满家具后,高为3.6米,宽为3.2米,请问这辆送家具的卡车能通过这个通道吗?为什么?
(2)如图2,若通道正中间有一个0.4米宽的隔离带,问一辆宽1.5米高3.8米的车能通过这个通道吗?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com