
【题目】如图1,某住宅社区在相邻两楼之间修建一个上方是一个半圆,下方是长方形的仿古通道.

(1)现有一辆卡车装满家具后,高为3.6米,宽为3.2米,请问这辆送家具的卡车能通过这个通道吗?为什么?
(2)如图2,若通道正中间有一个0.4米宽的隔离带,问一辆宽1.5米高3.8米的车能通过这个通道吗?为什么?
【答案】(1)能;(2)不能.
【解析】
(1)作弦EF∥AD,OH⊥EF于H,连接OF,在直角△OFH中,根据三角函数就可以求出OH,求出隧道的高.即可得到结论;
(2)同(1)求得HF和HM,然后求得MF后与1.5米比较即可.
(1)如图,设半圆O的半径为R,则R=2,作弦EF∥AD,且EF=3.2,OH⊥EF于H,连接OF,由OH⊥EF,∴HF=![]() EF=1.6m.
EF=1.6m.
又∵OH![]() 1.2,∴OH+AB=1.2+2.6=3.8>3.6,∴这辆卡车能通过此隧道;
1.2,∴OH+AB=1.2+2.6=3.8>3.6,∴这辆卡车能通过此隧道;
(2)如图2,当车高3.8米时,OH=3.8﹣2.6=1.2米,此时HF![]() 1.6米.
1.6米.
∵通道正中间有一个0.4米宽的隔离带,∴HM=0.2米,∴MF=HF﹣HM<1.5米,∴不能通过.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
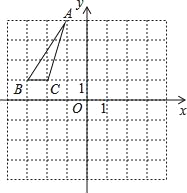
【题目】在如图所示的平面直角坐标系中,△ABC的三个顶点都在小正方形的顶点处,请结合图完成下列各题:
(1)写出tan∠ABC;AB的值;(结果保留根号).
(2)将△ABC绕原点O旋转180°,画出旋转对应的△A′B′C′,并求直线A′C′的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,港口A在观测站O的正东方向,OA=4.某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为____.

查看答案和解析>>
科目:初中数学 来源: 题型:
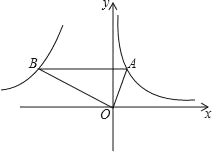
【题目】如图,Rt△ABO中,∠AOB=90°,点A在第一象限,点B在第二象限,且AO:BO=1:2,若经过点A的反比例函数解析式为y=![]() ,则经过点B(x,y)的反比例函数解析式为( )
,则经过点B(x,y)的反比例函数解析式为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
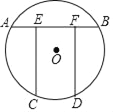
【题目】如图,为一圆洞门.工匠在建造过程中需要一根横梁AB和两根对称的立柱CE、DF来支撑,点A、B、C、D在⊙O上,CE⊥AB于E,DF⊥AB于F,且AB=2![]() ,EF=
,EF=![]() ,
,![]() =120°.
=120°.
(1)求出圆洞门⊙O的半径;
(2)求立柱CE的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
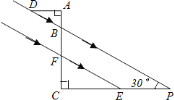
【题目】如图,某一时刻太阳光从教室窗户射入室内,与地面的夹角![]() 为
为![]() ,窗户的一部分在教室地面所形成的影长
,窗户的一部分在教室地面所形成的影长![]() 为
为![]() 米,窗户的高度
米,窗户的高度![]() 为
为![]() 米.求窗外遮阳蓬外端一点
米.求窗外遮阳蓬外端一点![]() 到教室窗户上椽的距离
到教室窗户上椽的距离![]() .(参考数据:
.(参考数据:![]() ,结果精确
,结果精确![]() 米)
米)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,反比例函数![]() (x>0)与正比例函数y=kx、
(x>0)与正比例函数y=kx、 ![]() (k>1)的图象分别交于点A、B,若∠AOB=45°,则△AOB的面积是________.
(k>1)的图象分别交于点A、B,若∠AOB=45°,则△AOB的面积是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某科技开发公司研制出一种新型产品,每件产品的成本为2400元,销售单价定为3000元.在该产品的试销期间,为了促销,鼓励商家购买该新型产品,公司决定商家一次购买这种新型产品不超过10件时,每件按3000元销售;若一次购买该种产品超过10件时,每多购买一件,所购买的全部产品的销售单价均降低10元,但销售单价均不低于2600元.
(1)商家一次购买这种产品多少件时,销售单价恰好为2600元?
(2)设商家一次购买这种产品x件,开发公司所获的利润为y元,求y(元)与x(件)之间的函数关系式,并写出自变量x的取值范围.
(3)该公司的销售人员发现:当商家一次购买产品的件数超过某一数量时,会出现随着一次购买的数量的增多,公司所获的利润反而减少这一情况.为使商家一次购买的数量越多,公司所获的利润最大,公司应将最低销售单价调整为多少元(其它销售条件不变)?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com