
【题目】如图,港口A在观测站O的正东方向,OA=4.某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为____.

科目:初中数学 来源: 题型:
【题目】一个各位数字都不为0的三位正整数N,现从它的百位、十位、个位上的数字中任意选择两个数字组成两位数若所有这些两位数的和等于这个三位数本身,则称这个三位数为本原数”例如:132,选择百位数字1和十位数字3所组成的两位数为:13和31;选择百位数字1和个位数字2所组成的两位数为:12和21;选择十位数字3和个位数字2所组成的两位数为:32和23,因为13+31+12+21+32+23=132,所以132是“本原数”
(1)判断123是不是“本原数”?请说明理由;
(2)一个三位正整数,若它的十位数字等于百位数字与个位数学的和,则称这样的三位数为“和中数”.若一个各位数字都不为0的“和中数”![]() 是“本原数”,求z与x的函数关系.
是“本原数”,求z与x的函数关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
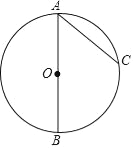
【题目】如图,AB是⊙O的直径,C是⊙O上一点,连接AC.过点B作⊙O的切线,交AC的延长线于点D,在AD上取一点E,使AE=AB,连接BE,交⊙O于点F.
请补全图形并解决下面的问题:
(1)求证:∠BAE=2∠EBD;
(2)如果AB=5,sin∠EBD=![]() .求BD的长.
.求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=k1x+b的图象与反比例函数y2=![]() 的图象相交于A,B两点,与x轴交于点C,与y轴交于点D,点B的坐标是(m,-4),连接AO,AO=5,sin∠AOC=
的图象相交于A,B两点,与x轴交于点C,与y轴交于点D,点B的坐标是(m,-4),连接AO,AO=5,sin∠AOC=![]() .
.
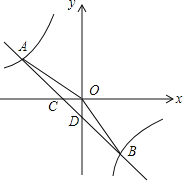
(1)求反比例函数的解析式;
(2)连接OB,求△AOB的面积;
(3)请直接写出当x<m时,y2的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() 的图象与一次函数
的图象与一次函数![]() 的图象交于点A(1,4)和点B
的图象交于点A(1,4)和点B
(![]() ,
,![]() ).
).

(1)求这两个函数的表达式;
(2)观察图象,当![]() >0时,直接写出
>0时,直接写出![]() >
>![]() 时自变量
时自变量![]() 的取值范围;
的取值范围;
(3)如果点C与点A关于![]() 轴对称,求△ABC的面积.
轴对称,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
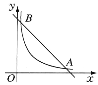
【题目】如图,在直角坐标系中,直线y=6-x与双曲线y=![]() (x>0)的图象相交于点A,B,设点A的坐标为(m,n),那么以m为长、n为宽的矩形的面积和周长分别为( )
(x>0)的图象相交于点A,B,设点A的坐标为(m,n),那么以m为长、n为宽的矩形的面积和周长分别为( )
A. 4,6 B. 4,12 C. 8,6 D. 8,12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC和△DEF满足下列条件,其中能使△ABC与△DEF相似的是( )
A. AB=c,AC=b,BC=a,DE=![]() ,EF=
,EF=![]() ,DF=
,DF=![]()
B. AB=1,AC=1.5,BC=2,DE=12,EF=8,DF=1
C. AB=3,AC=4,BC=6,DE=12,EF=8,DF=6
D. AB=![]() ,AC=
,AC=![]() ,BC=
,BC=![]() ,DE=
,DE=![]() ,EF=3,DF=3
,EF=3,DF=3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,某住宅社区在相邻两楼之间修建一个上方是一个半圆,下方是长方形的仿古通道.

(1)现有一辆卡车装满家具后,高为3.6米,宽为3.2米,请问这辆送家具的卡车能通过这个通道吗?为什么?
(2)如图2,若通道正中间有一个0.4米宽的隔离带,问一辆宽1.5米高3.8米的车能通过这个通道吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线与直线均过原点,直线经过抛物线的顶点(2,4),则下列说法:①当0<x<2时,y2>y1;②y2随x的增大而增大的取值范围是x<2;③使得y2大于4的x值不存在; ④若y2=2,则x=2﹣![]() 或x=1.
或x=1.
其中正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com